Right here, x, y, and z are unknowns, and a₁, b₁, c₁, d₁, a₂, b₂, c₂, d₂, a₃, b₃, c₃, d₃ are constants.
Since we now have three variables, the equations symbolize planes in a 3D house as a substitute of traces. The answer is the place all three planes intersect.
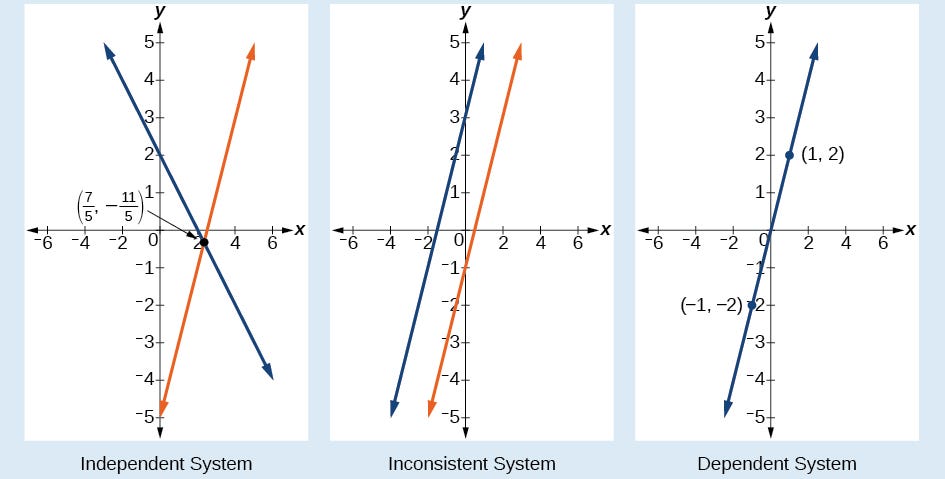
1️⃣ (a) Distinctive Resolution — The three planes intersect at a single level 🟢
2️⃣ (b) Infinite Options — The planes overlap or type a standard line/airplane ♾️ (c)No Resolution — The planes are parallel or by no means meet ❌
3️⃣ (c) No Resolution — The planes are parallel or by no means meet ❌
- Graphical Visualization (3D Plotting) 🔍
- Substitution & Elimination Methodology 🔄
- Matrix Strategies (Row Discount, Determinants, Inverse Matrix) 🧮
🔹 Instance:
x+y+z=6x + y + z = 6
2x−y+3z=142x — y + 3z = 14
y+2z=8y + 2z = 8
Fixing this technique offers x = 2, y = 1, z = 3 (Intersection level (2,1,3)).
🎯 Options of the App:
✅ 2D & 3D Graphs for straightforward understanding
✅ Actual-time manipulation of coefficients
✅ Mechanically detects whether or not the system has a distinctive, infinite, or no resolution
✅ Person-friendly interface for college students, information scientists, and engineers
🔗 Attempt It Right here: