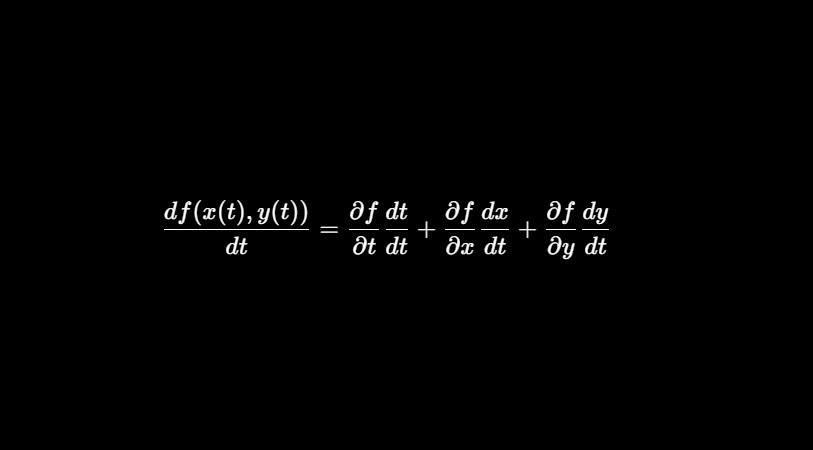article makes use of ideas from this sensible paper. For a deeper understanding of the arithmetic please seek advice from the paper. Right here we attempt to current the mathematics in a extra intuitive and express means, with some essential nuances highlighted.
1 Introduction
Discussions about Backpropagation typically say we use the ‘chain rule’ to derive the gradient wrt the weights after which go on to current a formulation like so: (frac{dy}{dx} = frac{dy}{dt} frac{dt}{dx}).
That is the single-variable chain rule and if we used it to calculate the loss wrt the gradients of every layer our calculations could be fallacious. This misrepresentation confuses the underlying arithmetic and undermines the true class of the equations. Actually, the chain rule used throughout backpropagation is a extra common case of the single-variable chain rule – referred to as the whole spinoff.
We’d like this extra common case as the issue we face throughout backpropagation is that every layer’s output kinds the enter to the following layer. Since every layer’s output can be influenced by its weights which means the weights (the values we wish to tweak) not directly affect the inputs to the following layer. Thus, to search out the gradient of the fee with respect to the weights of a layer (the motivation behind backprop) we should take into consideration how the weights in a layer affect the values of successive layers all the way in which right down to the ultimate layer the place the fee is evaluated. We’ll focus on this concern under.
One other problem we face is that every hidden layer’s output is a vector of values (there are a number of neurons in a layer), thus we’d like some approach to take into consideration all of the derivatives of the layer without delay with out having to calculate each as a separate operation.
On this article we are going to see how the vector chain rule helps resolve each these issues.
First, we deal with explaining the total-derivative and why it’s incorrect to current it as the only variable chain rule for its utility in backprop. We additionally present how the vector chain rule implements the total-derivative equation. Subsequent, we current some notation and describe the ahead cross in a neural community. Lastly, we derive the gradients for the weights in our community wrt to the fee and introduce some key ideas of the derivation as simplifications that make it doable to compute such big dependency graphs by means of some intelligent linear algebra and Calculus.
The vector chain rule we are going to present covers all instances of the chain rule so that it’ll work for the single-variable case too. That is complicated as you can’t inform which utility of the chain rule is being utilized in a selected operation. We make express once we do truly use the single-variable total-derivative chain rule over the single-variable chain rule.
Observe: There are various comparable factors of confusion, we spotlight these all through the doc.
To assist the reader observe alongside the mathematics behind the backpropagation algorithm we additionally present a full implementation in Numpy code utilizing the iris dataset.
2 Preliminaries
Implementations of the backprop equations use vector calculus to carry out extremely optimised computations to derive gradients of all weights in a layer in a single step.
The vector calculus we’d like requires some data in regards to the following.
Vital: All through this doc, lowercase letters in daring font similar to (mathbf{x}) are vectors and people in italics font like (x) are scalars. (x_i) is the (i)’th component of vector (mathbf{x}) and is in italics as a result of a single vector component is a scalar. Uppercase italicised letters like (W) point out a matrix. We use the notation (A * B) to indicate the element-wise multiplication between (A) and (B).
2.0.1 Partial derivatives
The partial spinoff of a multivariable operate with respect to one among its variables is its charge of change with respect to that particular variable, whereas holding all different variables fixed. Suppose we’ve got a operate:
[f(x,y) = 2xy^3]
We are able to compute its spinoff with respect to every of its parameters, treating the others as constants and checklist them out:
[ frac{partial f}{partial x} = 2y^3]
[frac{partial f}{partial y} = 6xy^2 ]
Thus, the partial spinoff of the operate with respect to (x), performs the standard scalar spinoff holding all different variables fixed. We do the identical for the partial spinoff with respect to (y).
2.0.2 The Jacobian Matrix
Once we gather the gradients (partials) of a vector-valued operate (capabilities that return a vector as their end result) or a vector of (m) scalar-valued capabilities and stack them on high of one another we’ve got a Jacobian matrix.
Take into account a operate (mathbf{f}(x,y)) that takes a number of scalar inputs (on this case, (x) and (y)) and produces a number of scalar outputs, that are then organised right into a vector.
Let’s say our operate (mathbf{f}) produces two scalar outputs, (f_1(x,y)) and (f_2(x,y)) . The Jacobian could be represented as:
[Deltamathbf{f} = begin{bmatrix} Delta f_1(x,y) Delta f_2(x,y) end{bmatrix} = begin{bmatrix} frac{partial f_1}{partial x} & frac{partial f_1}{partial y} frac{partial f_2}{partial x} & frac{partial f_2}{partial y} end{bmatrix}] Every row accommodates the partials of one of many output capabilities wrt to the variables (x) and (y). The Jacobian organises the partials of a number of capabilities by stacking them to offer a matrix that describes the general sensitivity of the output vector to modifications within the enter vector.
2.1 The Whole Spinoff
With the stipulations coated we will now introduce the idea of the total-derivative. You will need to perceive the idea to completely grasp the backpropagation equations introduced in a while.
We start by stating the single-variable chain guidelines applicability for capabilities like (f(g(x))) the place the spinoff is solely (f'(g(x)) * g'(x)), or in different phrases:
[frac{df(g(x))}{dx} = frac{df}{dg} frac{dg}{dx}]
Nonetheless, what occurs if we’ve got a operate like (f(x(t),y(t))) ?
For this operate, we see that small modifications in (t) have an effect on (f) not directly (by means of (x) and (y)) . Because the intermediate capabilities are capabilities of the identical variable we’ve got to account for every change relative to its contribution to the change in (f).
To get the gradient of (f) wrt to (t), the regulation of whole derivatives states that:
[frac{df(x(t),y(t))}{dt} = frac{partial f}{partial t}frac{dt}{dt} + frac{partial f}{partial x}frac{dx}{dt} + frac{partial f}{partial y}frac{dy}{dt}]
In our case, (f) just isn’t instantly a operate of (t) so we’ve got (frac{df}{dt} frac{dt}{dt} = 0).
The equation could be seen as a weighted sum of the contribution of (t) to the general worth of (f) by means of (x) and (y). That’s (frac{partial{f}}{partial{t}}), (frac{partial{f}}{partial{x}}) and (frac{partial{f}}{partial{y}}) could be seen as weighting the general contribution of (t) with respect to every of the parameters of (f).
The derivatives (frac{dt}{dt}), (frac{dx}{dt}) and (frac{dy}{dt}) are extraordinary derivatives since every parameter is a operate of a single variable (t).
Vital: If (x) was solely a operate of (t) (or (y)) the phrases involving (frac{dy}{dt}) change into (0) and thus the total-derivative formulation reduces to the single-variable chain rule.
We are able to generalise this formulation additional by representing the parameters (x) and (y) as parts of a vector (mathbf{u}) in order that:
[f(mathbf{u}(t)) = f(x(t),y(t))]
Now if we substitute (u_{n+1}) as an alias for (t) we will write:
[ Delta f(mathbf{u}(t)) = frac{df}{dt} = sum^{n+1}_{i = 1} frac{partial f}{partial u_i} frac{partial u_i}{partial t}]
Discover the refined distinction in notation from the single-variable case. The entire derivatives are proven as partial derivatives as a result of (f) and its parameters (u_i) are capabilities of a number of variables.
The summation seems like a vector dot product (or matrix multiplication if (f) was a vector operate (mathbf{f})). Utilizing this reality, we will denote the total-derivative when it comes to two different Jacobians:
[Delta f(mathbf{u}(t)) = frac{partial f}{partial mathbf{u}} frac{partial mathbf{u}}{partial t}]
the place the Jacobian (frac{partial f}{partial mathbf{u}}) is matrix multiplied by the Jacobian (frac{partial mathbf{u}}{partial t}) to provide the full spinoff of (f) wrt to (t). Right here the partial spinoff notation is critical as a result of (mathbf{u}) turns into a vector of capabilities of (t).
This formulation is named the vector chain rule. The wonder is that the vector chain rule takes into consideration the total-derivative whereas sustaining the identical notational simplicity of the single-variable chain rule.
Examine the vector chain rule above to the single-variable chain rule:
[Delta f(u(t)) = frac{df}{du}frac{du}{dt}]
and we see the doable motive for a number of the confusion.
2.2 Ahead cross and a few notation
Let’s transfer on to describing the ahead cross in a neural community.
Single neuron output
A neuron’s output (z) is a weighted sum of its inputs and a bias time period.
Thus we will write:
[ z = x_{1}w_1 + x_{2}w_2 + cdots + x_{n}w_n + b = sum_{i=1}^{n} w_i x_i ]
If we outline vectors (mathbf{w}) and (mathbf{x}) to signify every (w_i) , (x_i) worth: (mathbf{w} = start{bmatrix} w_1 , w_2 , cdots, w_n finish{bmatrix}) and (mathbf{x} = start{bmatrix} x_1 , x_2 , cdots, x_n finish{bmatrix}) the place (mathbf{w}) is the neurons weight vector and (mathbf{x}) is the vector of its inputs , we will then write the weighted sum as a dot product of the 2 vectors (mathbf{x}) and (mathbf{w}):
[z = mathbf{w} cdot mathbf{x} + b]
An activation operate is then utilized to the output (z) to introduce non-linearity. Let’s denote the output after activation of the neuron as (a). Then:
[a = sigma(z)]
the place (sigma) denotes the activation operate.
Layer output
In follow, a layer accommodates a number of neurons in order that (z) is a vector (mathbf{z}), every with its personal randomly initialised weight vector.
Because of this as a substitute of a vector of weights (mathbf{w}) we’ve got a matrix of weights (W), the place the rows are given by the variety of neurons within the present layer (i) and the columns by the variety of neurons within the earlier layer (j).
Vital: Enter vector (mathbf{x}) could be a matrix (X) when contemplating a number of observations (a batch) for a single cross by means of our community.
Let’s denote the weights of a layer in matrix type:
[W = begin{bmatrix} mathbf{w}_1 mathbf{w}_2 vdots mathbf{w}_i end{bmatrix} = begin{bmatrix} w_{1,1} & w_{1,2} & cdots & w_{1,j} w_{2,1} & w_{2,2} & cdots & w_{2,j} vdots & vdots & ddots & vdots w_{i,1} & w_{i,2} & cdots & w_{i,j} end{bmatrix}]
Observe that every (mathbf{w}_i) vector has a set of (j) parts similar to the variety of neurons within the earlier layer. Because of this (mathbf{z}_i) takes a vector of parameters (mathbf{w}_i) with size (|j|).
Then for all of the neurons in a layer (L) we’ve got a vector (mathbf{z}) the place:
[mathbf{z}(W,mathbf{x},mathbf{b}) = begin{bmatrix} z_1 z_2 vdots z_i end{bmatrix} = begin{bmatrix} mathbf{w}_1 . mathbf{x} + b_1 mathbf{w}_2 . mathbf{x} + b_2 vdots mathbf{w}_i . mathbf{x} + b_i end{bmatrix}]
This may be written succinctly as a matrix multiplication between (mathbf{x}) and (W):
[mathbf{z}(W,mathbf{x},mathbf{b}) = mathbf{x}W^T + mathbf{b}]
You will need to do not forget that every neuron in a neural community has its personal weight vector, in order that ({z}_1) is solely a operate of (mathbf{w}_1), (z_2) of (mathbf{w}_2) and so forth.
Vital: The vector of inputs (mathbf{x}) is solely the outputs of the neurons from the earlier layer (or the variety of options for the primary layer). Thus for all layers however the enter layer: [mathbf{x}^l = mathbf{a}^{l-1}]
Layer output after activation
Lastly, for our community to have the ability to clarify extra complicated phenomena we introduce non-linearity to a neuron’s output. We do that by making use of a nonlinear operate over the outputs (mathbf{z}) of the neurons in layer (l).
The outputs of a layer (l) can then be represented as:
[mathbf{a}^{[l]}(mathbf{z}) = start{bmatrix} sigma(z_1) sigma(z_2) vdots sigma(z_i ) finish{bmatrix} ]
The place the activation operate (sigma) is utilized component smart to the layers pre-activation output (mathbf{z}).
Consequently, the activation of a layer can then be written as a operate of (W), (mathbf{x}) and (mathbf{b}):
[mathbf{a}^{[l]}(W,mathbf{x},mathbf{b}) = start{bmatrix} sigma(mathbf{w}^{[l]}_1 . mathbf{x} + b_1) sigma(mathbf{w}^{[l]}_2 . mathbf{x} + b_2) vdots sigma(mathbf{w}^{[l]}_i . mathbf{x} + b_i) finish{bmatrix}qquad{(1)}]
Discover how the output of a layer resembles the vector operate (mathbf{f}) from the outline of a Jacobian matrix in sec. 2.0.2.
Actually, every layer in a neural internet could be seen as a vector operate that receives a vector of inputs and maps (transforms) them to an output vector. The dimensionality of the output vector is decided by the variety of neurons in that layer.
In different phrases, every neuron (i) takes enter vectors (mathbf{x}) and (mathbf{w}_i) and outputs a scalar worth (z_i), the place every neurons output type the weather of the vector output of the layer.
Observe: This may be outlined as a linear transformation of the inputs or extra exactly an affine transformation as it’s a linear transformation (xW^T) adopted by a translation (addition of the (mathbf{b}) time period).
Lastly, a fascinating attribute of activation capabilities, along with their non-linear nature, is that their derivatives could be conveniently calculated (typically) based mostly on the operate’s worth itself. This make the calculation of gradients extra computationally environment friendly. We’ll discover this intimately in sec. 3.2.2.
Now that we perceive the fundamentals of the feed-forward mechanism, let’s deal with the derivation of the backpropagation equations.
3 The Gradient of the Value Operate
Throughout backpropagation we’re fascinated with discovering the gradient (charge of change) of the fee operate with respect to the weights in every layer of our neural internet. This may permit us to replace the weights within the path of decrease price after every cross by means of our neural community. Merely put, because the gradient will inform us the values of the ‘slopes’ that produce higher price we replace the weights in the wrong way as a substitute to minimise it.
As touched upon earlier, we have to account for the general change in loss by contemplating the impact every of the weights and biases in our neural community have on subsequent layers in our community in the course of the ahead cross.
We restrict our deal with the derivation of the gradient with respect to the weights on this article (extending the idea for the bias phrases is trivial as soon as that is grasped – see how the bias time period is dealt with in our implementation).
For our rationalization we think about the community proven in fig. 1. We’ll deal with the derivation of the gradients of the weights for the output layer and the hidden layers individually as they require barely completely different strategies conceptually.
To get a extra intuitive really feel of the oblique dependencies concerned we start by denoting the fee as a composite operate.
3.1 Value as a composite operate
3.1.1 Remaining layer
The price of a community could be seen as a operate of two parameters in order that:
[ C(mathbf{y},mathbf{hat{y}})]
the place (mathbf{y}) is the vector of true labels and (mathbf{hat{y}}) a vector of our corresponding predictions.
Utilizing our notation as earlier than (eq. 1) and making use of them to our neural community in fig. 1 , let (mathbf{a}_L) be a vector of the ultimate layers ((L)) outputs, in order that:
[mathbf{a}_L(W_L,mathbf{a}_{L-1}) = begin{bmatrix} sigma(z_1(mathbf{w}_1,mathbf{a}_{L-1})) sigma(z_2(mathbf{w}_2,mathbf{a}_{L-1})) sigma(z_3(mathbf{w}_3,mathbf{a}_{L-1})) end{bmatrix}]
Treating (mathbf{a}_{L}) as a vector operate as we’ve got, we see that it’s a operate of two parameters (W_L) and (mathbf{a}_{L – 1}) (leaving out the bias time period (mathbf{b})).
For the reason that activation of the final layer (L) is the prediction of our mannequin (mathbf{hat{y}} = mathbf{a}_L) we will signify the fee as a composite operate of the earlier layers activation :
[C(mathbf{y},mathbf{hat{y}}) = C(mathbf{y},mathbf{a}_L(W_L,mathbf{a}_{L-1}))qquad{(2)}]
Expanded this might appear to be (we omit the superscript (L) for the final layer parameters (z_i), (mathbf{w}_i)):
[C(mathbf{y},sigma(z_1(mathbf{w}_1,mathbf{a}_{L-1})),sigma(z_2(mathbf{w}_2,mathbf{a}_{L-1})),sigma(z_3(mathbf{w}_3,mathbf{a}_{L-1})))qquad{(3)}]
Within the last layer’s weights, this equation reveals a direct path of affect: every weight vector (mathbf{w}_i) impacts the fee solely by means of its related (z_i). Consequently, calculating the gradient with respect to those weights primarily requires making use of the vector extension of the single-variable chain rule, with out the necessity for the full spinoff.
3.1.2 Hidden layer(s)
For the hidden layer(s) we basically have to look (l) layers ‘deeper’ to get the weights of layer (l) with respect to the fee. In our instance in fig. 1, we’ve got one hidden layer whose outputs are denoted (mathbf{a}_{L-1}).
We are able to categorical eq. 2 with the hidden layer weights included:
[C(mathbf{y},mathbf{a}_L(W_L,mathbf{a}_{L-1}(W_{L-1},mathbf{a}_{L-2})))qquad{(4)}]
Observe: Now we have a single hidden layer in our community so (mathbf{a}_{L-2} = mathbf{x}), the place (mathbf{x}) is a vector of enter options.
In eq. 4 we discover that the weights of every neuron within the hidden layer (L-1) have an effect on the inputs to every neuron within the last layer (L). As a consequence, (W_{L-1}) impacts the fee (C) by means of a number of paths (mathbf{a}_L).
This inter-dependence necessitates using the total-derivative to compute (frac{partial C}{partial mathbf{a}_{L-1}}) and subsequently (frac{dC}{dW_{L-1}}) for every hidden layer (l), the values we are literally fascinated with.
3.2 Discovering the gradients
Now that we’ve got a clearer understanding of the capabilities we have to resolve for, we deal with deriving the backpropagation equations and highlighting the completely different purposes of the chain rule which are used. We additionally cowl how the pre-computation of gradients permits us to implement the algorithm. All examples think about a single commentary (stochastic gradient descent) to simplify the notation.
3.2.1 Remaining layer
To reiterate, the duty is for us to search out the gradient of the fee with respect to all the weights within the weight matrix (W_{L}). In our instance, this consists of (15) ((i occasions j)) weights in all for the ultimate layer.
We have to discover: [frac{dC}{dW_L}]
given the fee equation for the ultimate layers weights in eq. 3.
As we’ve got seen, the total-derivative just isn’t required to calculate the gradient of the fee wrt the ultimate layers’ weights. Right here we merely want to make use of the single-variable chain rule prolonged to vectors.
Let’s write out the partials (Jacobians) we’d like, to additionally assist visualise their dimensions:
I.
The gradient of the fee wrt to the predictions of our mannequin (mathbf{a}_L):
[frac{partial C}{partial mathbf{a}_{L}} = begin{bmatrix} frac{partial C}{partial a^{[L]}_{1}} & frac{partial C}{partial a^{[L]}_2} & frac{partial C}{partial a^{[L]}_3} finish{bmatrix}]
II.
The gradient of the predictions of our mannequin wrt the pre-activation outputs (mathbf{a}_L):
[frac{partial mathbf{a}_{L}}{partial mathbf{z}_{L}} = begin{bmatrix} frac{partial a_1^{[L]}}{partial z_1^{[L]}} & frac{partial a_1^{[L]}}{partial z_2^{[L]}} & frac{partial a_1^{[L]}}{partial z_3^{[L]}} frac{partial a_2^{[L]}}{partial z_1^{[L]}} & frac{partial a_2^{[L]}}{partial z_2^{[L]}} & frac{partial a_2^{[L]}}{partial z_3^{[L]}} frac{partial a_3^{[L]}}{partial z_1^{[L]}} & frac{partial a_3^{[L]}}{partial z_2^{[L]}} & frac{partial a_3^{[L]}}{partial z_3^{[L]}} finish{bmatrix}]
Right here, the off-diagonal parts go to zero since (a_k) just isn’t a operate of (z_i) when (i neq ok) so we’ve got:
[frac{partial mathbf{a}_{L}}{partial mathbf{z}_{L}} = diag(frac{partial mathbf{a}_{L}}{partial mathbf{z}_{L}}) = begin{bmatrix} frac{partial a_1^{[L]}}{partial z_1^{[L]}} & frac{partial a_2^{[L]}}{partial z_2^{[L]}} & frac{partial a_3^{[L]}}{partial z_3^{[L]}}finish{bmatrix}]
III.
Subsequent, for the pre-activation outputs with respect to the weights (frac{partial mathbf{z}_L}{partial W_{L}}) we’ve got:
[ frac{partial mathbf{z}_{L}}{partial W_{L}} = begin{bmatrix} frac{partial z_1^{[L]}}{partial mathbf{w_1}^{[L]}} frac{partial z_2^{[L]}}{partial mathbf{w_2}^{[L]}} frac{partial z_3^{[L]}}{partial mathbf{w_3}^{[L]}} finish{bmatrix} = start{bmatrix}frac{partial z_1^{[L]}}{partial w_{11}^{[L]}} & frac{partial z_1^{[L]}}{partial w_{12}^{[L]}} & frac{partial z_1^{[L]}}{partial w_{13}^{[L]}} & frac{partial z_1^{[L]}}{partial w_{14}^{[L]}} & frac{partial z_1^{[L]}}{partial w_{15}^{[L]}} frac{partial z_2^{[L]}}{partial w_{21}^{[L]}} & frac{partial z_2^{[L]}}{partial w_{22}^{[L]}} & frac{partial z_2^{[L]}}{partial w_{23}^{[L]}} & frac{partial z_2^{[L]}}{partial w_{24}^{[L]}} & frac{partial z_2^{[L]}}{partial w_{25}^{[L]}} frac{partial z_3^{[L]}}{partial w_{31}^{[L]}} & frac{partial z_3^{[L]}}{partial w_{32}^{[L]}} & frac{partial z_3^{[L]}}{partial w_{33}^{[L]}} & frac{partial z_3^{[L]}}{partial w_{34}^{[L]}} & frac{partial z_3^{[L]}}{partial w_{35}^{[L]}} finish{bmatrix}]
Every column corresponds to a weight vector connecting a neuron (j) from the earlier layer to neurons (i) within the present layer.
IV.
Lastly, to search out the intermediate partial (frac{partial C}{partial mathbf{z}_L}) we have to carry out an element-wise multiplication between (frac{dC}{dmathbf{a}_L}) and (frac{dmathbf{a}_L}{dmathbf{z}_L}) as all we’d like is the single-variable chain rule. It is because there are not any oblique dependencies between layers to account for :
[frac{partial C}{partial mathbf{z}_L} = frac{partial C}{partial mathbf{a}_L} * frac{partial mathbf{a}_L}{partial mathbf{z}_L} = begin{bmatrix} frac{partial C}{partial a^{[L]}_{1}} & frac{partial C}{partial a^{[L]}_2} & frac{partial C}{partial a^{[L]}_3} finish{bmatrix} * start{bmatrix} frac{partial a_1^{[L]}}{partial z_1^{[L]}} & frac{partial a_2^{[L]}}{partial z_2^{[L]}} & frac{partial a_3^{[L]}}{partial z_3^{[L]}}finish{bmatrix} ]
Now that we’ve got discovered our partials we will use the chain rule for vectors to specific the Jacobian we’re fascinated with:
[frac{dC}{dW_{L}} = (frac{partial C}{partial mathbf{a}_L} * frac{partial mathbf{a}_L}{partial mathbf{z}_L}) otimes frac{partial mathbf{z}_L}{partial W_{L}} = frac{partial C}{partial mathbf{z}_{L}} otimes frac{partial mathbf{z}_{L}}{partial W_{L}} = begin{bmatrix} frac{partial C}{partial z_1^{[L]}} frac{partial z_1^{[L]}}{partial w_{11}^{[L]}} & frac{partial C}{partial z_2^{[L]}} frac{partial z_2^{[L]}}{partial w_{21}^{[L]}} & frac{partial C}{partial z_3^{[L]}} frac{partial z_3^{[L]}}{partial w_{31}^{[L]}} frac{partial C}{partial z_1^{[L]}} frac{partial z_1^{[L]}}{partial w_{12}^{[L]}} & frac{partial C}{partial z_2^{[L]}} frac{partial z_2^{[L]}}{partial w_{22}^{[L]}} & frac{partial C}{partial z_3^{[L]}} frac{partial z_3^{[L]}}{partial w_{32}^{[L]}} frac{partial C}{partial z_1^{[L]}} frac{partial z_1^{[L]}}{partial w_{13}^{[L]}} & frac{partial C}{partial z_2^{[L]}} frac{partial z_2^{[L]}}{partial w_{23}^{[L]}} & frac{partial C}{partial z_3^{[L]}} frac{partial z_3^{[L]}}{partial w_{33}^{[L]}} frac{partial C}{partial z_1^{[L]}} frac{partial z_1^{[L]}}{partial w_{14}^{[L]}} & frac{partial C}{partial z_2^{[L]}} frac{partial z_2^{[L]}}{partial w_{24}^{[L]}} & frac{partial C}{partial z_3^{[L]}} frac{partial z_3^{[L]}}{partial w_{34}^{[L]}} frac{partial C}{partial z_1^{[L]}} frac{partial z_1^{[L]}}{partial w_{15}^{[L]}} & frac{partial C}{partial z_2^{[L]}} frac{partial z_2^{[L]}}{partial w_{25}^{[L]}} & frac{partial C}{partial z_3^{[L]}} frac{partial z_3^{[L]}}{partial w_{35}^{[L]}} finish{bmatrix}^T]
We’ll clarify the selection of operators quickly. For now, deal with the complexity of the calculation.
For a easy community like we’ve got, we would wish to compute the values of all of the required partials to get the gradient of the fee wrt the weights of the ultimate layer. We’d then have to repeat the method for the hidden layers weights. Moreover, throughout coaching we sometimes cross many batches of information by means of our community. For every batch, we have to carry out a ahead cross to calculate the fee and a backward cross to compute the gradients.
As community dimension grows, the computational burden rapidly escalates to an impractical degree. A key simplification arises from the truth that we will categorical these partial derivatives utilizing values we’ve got already decided.
3.2.2 Pre-computation of gradients
First, lets attempt to derive the partial of the weights wrt a single neuron output (z_i) after which see if we will prolong this to a vector of outputs (mathbf{z}). We omit the bias time period to deal with the spinoff of the dot-product operation:
[z_i = mathbf{w}_{i}^{[L]} cdot mathbf{a}^{[L-1]} = sum_{ok=1}^{n} (w_k a_k)]
Discover how we don’t index (mathbf{a^{[l-1]}}) it is because all (z_i) within the present layer share the identical enter vector, what modifications are the burden and bias vectors between every (z_i).
Then the spinoff of (z_i) wrt to a selected weight (w_j) is:
[frac{partial z_i}{partial w_j} = sum_{k=1}^{n}frac{partial}{partial w_j} (w_k a_k) = a_j]
The summation disappears as a result of (frac{partial}{partial w_j} w_k a_k) reduces to a continuing when (j neq ok), the spinoff of which is (0).
For the reason that result’s a scalar worth when (w) is scalar, to increase this to a vector of (mathbf{w}_i) we merely have:
[frac{partial z_i}{partial mathbf{w}_i} = begin{bmatrix} a_1^{[L-1]} & a_2^{[L-1]} & a_3^{[L-1]} & a_4^{[L-1]} & a_5^{[L-1]} finish{bmatrix} = mathbf{a}^{[L-1]} ]
That’s a considerably simpler computation because the activations have already been computed in the course of the ahead cross. This additionally means the gradients are shared throughout every (z_i). As an alternative of getting to search out (15) particular person partials we simply want to search out (5) which have already been computed!
This end result tells us that the gradient of the pre-activation output ((z_i)) of a neuron (i) wrt (w_{ij}) is the activation of the neuron (j) the burden originates from. This is smart because the gradient of (z_i) with respect to (w_{kj}) is (0) when (ok neq i) so the partials ought to merely be a vector of size (|j|) for every (z_i).
Every column of this matrix conceptually represents how a lot a small change within the weights in (mathbf{w}_i) impacts the output (z_i). To get the impact the change has on the fee (C) we might want to use the chain rule.
Now we will write:
[frac{partial C}{partial W_{L}} = frac{partial C}{partial mathbf{z}_{L}}^T otimes mathbf{a}_{L-1} = begin{bmatrix} frac{partial C}{partial z^{[L]}_{1}} frac{partial C}{partial z^{[L]}_2} frac{partial C}{partial z^{[L]}_3} finish{bmatrix} otimes start{bmatrix} a_1^{[L-1]} & a_2^{[L-1]} & a_3^{[L-1]} & a_4^{[L-1]} & a_5^{[L-1]} finish{bmatrix}]
Thus, the spinoff of the fee (the lack of our community) with respect to matrix (W_L) (by means of intermediate variables z) is a sq. matrix with parts computed utilizing the outer product. We explicitly use the outer-product to point the operation doesn’t use the total-derivative chain rule that the matrix-product operation introduces for the gradients of the hidden layer weights in a while (eq. 5).
Vital: A matrix multiplication between the partials (frac{partial C}{partial mathbf{z}_{L}} frac{partial mathbf{z}_{L}}{partial W_{L}}) is frequent when contemplating a number of observations (batch). This successfully sums alongside the partials for every commentary to get a complete contribution to the general loss. The matrix product is not used to compute the full spinoff on this case!
If we had been to broaden this operation for readability, the entire Jacobian would appear to be:
[frac{dC}{dW_{L}} = begin{bmatrix} frac{partial C}{partial z^{[L]}_{1}} a_1^{[L-1]} & frac{partial C}{partial z^{[L]}_{1}} a_2^{[L-1]} & frac{partial C}{partial z^{[L]}_{1}} a_3^{[L-1]} & frac{partial C}{partial z^{[L]}_{1}} a_4^{[L-1]} & frac{partial C}{partial z^{[L]}_{1}} a_5^{[L-1]} frac{partial C}{partial z^{[L]}_{2}} a_1^{[L-1]} & frac{partial C}{partial z^{[L]}_{2}} a_2^{[L-1]} & frac{partial C}{partial z^{[L]}_{2}} a_3^{[L-1]} & frac{partial C}{partial z^{[L]}_{2}} a_4^{[L-1]} & frac{partial C}{partial z^{[L]}_{2}} a_5^{[L-1]} frac{partial C}{partial z^{[L]}_{3}} a_1^{[L-1]} & frac{partial C}{partial z^{[L]}_{3}} a_2^{[L-1]} & frac{partial C}{partial z^{[L]}_{3}} a_3^{[L-1]} & frac{partial C}{partial z^{[L]}_{3}} a_4^{[L-1]} & frac{partial C}{partial z^{[L]}_{3}} a_5^{[L-1]} finish{bmatrix}]
Additional, because the price and activation capabilities are recognized and predetermined, the partial (frac{partial C}{partial mathbf{z}_L}) can often be expressed when it comes to the activation operate and the true labels themselves. For instance, the spinoff of the fee wrt its pre-activation inputs (mathbf{z}_L) is solely (mathbf{a}_L – mathbf{y}) when utilizing a softmax activation over the ultimate layer (given (mathbf{y}) is a one-hot encoded vector of true labels and the fee operate (C) is the cross-entropy loss).
The gradient of the weights of the ultimate layer wrt the fee can then be expressed as a sequence of matrix operations betweeen the Jacobians:
[frac{dC}{dW_L} = (frac{partial C}{partial mathbf{a}_L} * frac{partial mathbf{a}_L}{partial mathbf{z}_L}) otimes frac{partial mathbf{z}_L}{partial W_{L}} ]
3.2.3 Hidden layer(s)
Recall the fee written as a composite equation in eq. 4. We noticed that for every layer’s weight gradients we have to iteratively resolve the nested composite operate till we attain the enter layer.
Let’s visualise the Jacobians we have to resolve for layer (L-1) weights.
We’ve already written out the worth of (frac{partial C}{partial mathbf{z}_{L}}) earlier.
I.
For the pre-activation outputs (mathbf{z}_{L}) wrt inputs (mathbf{a}_{L -1}) we’ve got:
[frac{partial mathbf{z}_{L}}{partial mathbf{a}_{L-1}} = begin{bmatrix} frac{partial z_1^{[L]}}{partial a_1^{[L-1]}} & frac{partial z_1^{[L]}}{partial a_2^{[L-1]}} & frac{partial z_1^{[L]}}{partial a_3^{[L-1]}} & frac{partial z_1^{[L]}}{partial a_4^{[L-1]}} & frac{partial z_1^{[L]}}{partial a_5^{[L-1]}} frac{partial z_2^{[L]}}{partial a_1^{[L-1]}} & frac{partial z_2^{[L]}}{partial a_2^{[L-1]}} & frac{partial z_2^{[L]}}{partial a_3^{[L-1]}} & frac{partial z_2^{[L]}}{partial a_4^{[L-1]}} & frac{partial z_2^{[L]}}{partial a_5^{[L-1]}} frac{partial z_3^{[L]}}{partial a_1^{[L-1]}} & frac{partial z_3^{[L]}}{partial a_2^{[L-1]}} & frac{partial z_3^{[L]}}{partial a_3^{[L-1]}} & frac{partial z_3^{[L]}}{partial a_4^{[L-1]}} & frac{partial z_3^{[L]}}{partial a_5^{[L-1]}} finish{bmatrix}]
Utilizing the identical strategy of differentiation as we did for (frac{partial z}{partial mathbf{w}}) earlier, the spinoff of (mathbf{z}_l) wrt its inputs is solely given by the layer (l) weight matrix :
[frac{partial mathbf{z}_{L}}{partial mathbf{a}_{L-1}} = W_{L} = begin{bmatrix} w_{11} & w_{12} & w_{13} & w_{14} & w_{15} w_{21} & w_{22} & w_{23} & w_{24} & w_{25} w_{31} & w_{32} & w_{33} & w_{34} & w_{35} end{bmatrix}]
II.
Subsequent, we discover the intermediate partial (frac{partial C}{partial mathbf{a}_{L-1}}) (which is able to inform us how the hidden layers outputs have an effect on the ultimate price):
The explanation the computation differs from the ultimate layer is that every (z^{[L]}_i) receives all (a^{[L-1]}_j) as inputs.
As a consequence, to search out the intermediate partial (frac{partial C}{partial mathbf{a}_{L-1}}) utilizing the Jacobians (frac{partial C}{partial mathbf{z}_{L}}, frac{partial mathbf{z}_{L}}{partial mathbf{a}_{L-1}}) we should think about how every activation (a_j) in layer (L-1) influences the fee by means of its contribution to every (a_i) within the last layer (L) (by means of (z_i^L)).
This implies (as talked about in sec. 3.1.2) we’d like the full spinoff to search out the intermediate partial (frac{partial C}{partial mathbf{a}_{L-1}}).
Since we all know the total-derivative could be expressed as a matrix product, the calculation of (frac{partial C}{partial mathbf{a}_{L-1}}) could be written explicitly as:
[ frac{partial C}{partial mathbf{a}_{L-1}} = frac{partial C}{partial mathbf{z}_{L}} frac{partial mathbf{z}_{L}}{partial mathbf{a}_{L-1}} = frac{partial C}{partial mathbf{z}_{L}} W_{L} = begin{bmatrix} frac{partial C}{partial z_1^{[L]}} w_{11} + frac{partial C}{partial z_2^{[L]}} w_{21} + frac{partial C}{partial z_3^{[L]}} w_{31} frac{partial C}{partial z_1^{[L]}} w_{12} + frac{partial C}{partial z_2^{[L]}} w_{22} + frac{partial C}{partial z_3^{[L]}} w_{32} frac{partial C}{partial z_1^{[L]}} w_{13} + frac{partial C}{partial z_2^{[L]}} w_{23} + frac{partial C}{partial z_3^{[L]}} w_{33} frac{partial C}{partial z_1^{[L]}} w_{14} + frac{partial C}{partial z_2^s{[L]}} w_{24} + frac{partial C}{partial z_3^{[L]}} w_{34} frac{partial C}{partial z_1^{[L]}} w_{15} + frac{partial C}{partial z_2^{[L]}} w_{25} + frac{partial C}{partial z_3^{[L]}} w_{35} finish{bmatrix}^Tqquad{(5)}]
We now have the dependency ‘graph’ for the affect a small change within the activations of the hidden layer (mathbf{a}_{L-1}) have on the fee.
III.
For the spinoff of the hidden layers activations (a_i^{L-1}) wrt its pre-activation outputs (z_i^{L-1}) we have to first outline an activation operate. We use a ReLU activation, outlined as:
[sigma_{ReLU} = max(0,z_i^{L-1})]
Then the spinoff of the activation wrt to the pre-activation inputs of layer (L-1) is a matrix of (1)’s and (0)’s: [ frac{partial mathbf{a}_{L-1}}{partial mathbf{z}_{L-1}} = sigma_{ReLU}'(z_i^{L-1}) = begin{cases} 1 & text{if } z_i^{L-1} > 0 0 & text{if } z_i^{L-1} leq 0 end{cases}]
IV.
From earlier than we all know the gradient of the weights of a layer wrt its pre-activation outputs is solely the layers inputs. Since we’ve got a single hidden layer the inputs to it are the fashions enter options (mathbf{x}):
[frac{partial mathbf{z}_{L-1}}{partial W_{L-1}} = mathbf{x}]
Now that we’ve got discovered our Jacobians, all that’s left do is multiply out the corresponding partials utilizing the single variable chain-rule prolonged to vectors. It is because the total-derivative calculation in step II has already accounted for the oblique inter-layer dependencies. We now solely have to deal with the ‘native’ derivatives inside the hidden layer.
Lastly, we will signify the gradient of the fee wrt the weights in our hidden layer as a sequence of matrix operations:
[ frac{dC}{dW_{L-1}} = frac{partial C}{partial mathbf{z}_{L}}frac{partial mathbf{z}_{L}}{partial mathbf{a}_{L-1}} * frac{partial mathbf{a}_{L-1}}{partial mathbf{z}_{L-1}} otimes frac{partial mathbf{z}_{L-1}}{partial W_{L-1}} = ( frac{partial C}{partial mathbf{z}_{L}}W_{L} * frac{partial mathbf{a}_{L-1}}{partial mathbf{z}_{L-1}} ) otimes mathbf{x} ]
which could be written merely as:
[frac{dC}{dW_{L-1}} = frac{partial C}{partial mathbf{z}_{L-1}} otimes mathbf{x}]
By caching the worth of the intermediate partial (frac{partial C}{partial mathbf{z}_{L – l}}) for all hidden layers (l) we will recursively apply this technique to every hidden layers weights.
Discover once more how carefully this resembles the easy single-variable chain rule if the operators between the Jacobians weren’t written out explicitly. The type of the equation is comparable as a result of the matrix product operation takes under consideration the full spinoff in its computation.
4 Conclusion
On this article, we’ve got demonstrated how the frequent illustration of the single-variable chain rule, as utilized to the backpropagation equations, is deceptive or incorrect. We highlighted the need of utilizing the total-derivative (a extra common type of the chain rule) as a result of composite nature of the backpropagation equations we’re fixing and defined how the vector chain rule implements this whole spinoff by means of matrix operations.
Moreover, we explored why the completely different chain guidelines are sometimes conflated in explanations. A number of components contribute to this confusion:
- The vector chain rule employs notation that resembles the single-variable chain rule.
- In lots of particular cases, similar to when figuring out the weights of the ultimate layer (as mentioned in sec. 3.2.1), the vector chain rule simplifies to the single-variable chain rule.
- The usage of matrix multiplication to mixture gradients from a batch of observations contrasts with its position in implementing the full spinoff in different components of the backpropagation equations.
These components make it difficult to persistently determine which chain rule is being utilized.
Past addressing the confusion, our derivation additionally revealed the important thing concepts that make the backpropagation equations tractable:
- The matrix product operation between Jacobians takes under consideration the full spinoff.
- Computation is basically pointless for the required partials:
- the gradient of the weighted sum of a layer wrt its inputs is solely given by the layers weight matrix.
- equally, the gradient of the weighted sum of a layer wrt its weights is given by the earlier layers activation.
- an activation operate is chosen in order that the gradient of the output of a layer (mathbf{a}_L) wrt to its pre-activation output (mathbf{z}_L) can typically be expressed when it comes to the activation operate itself.
- Calculations concerned find the gradient of the fee wrt a layers weights helps us discover the gradient of the fee with respect to the earlier layers weights till we attain the enter layer. Like this, backpropagation recursively finds the gradients for every layer.
These concepts simplify the mathematics and certainly make backpropagation computationally doable!
Lastly, to confirm our understanding we applied our personal neural internet in numpy and educated it to categorise species of iris given its sepal and petal size and width. You possibly can attempt it out your self on this colab notebook.