A Simple Implementation of the Attention Mechanism from Scratch

The Attention Mechanism is commonly related to the transformer structure, nevertheless it was already utilized in RNNs. In Machine Translation or MT (e.g., English-Italian) duties, once you need to predict the subsequent Italian phrase, you want your mannequin to focus, or concentrate, on crucial English phrases which can be helpful to make a great translation.

I can’t go into particulars of RNNs, however consideration helped these fashions to mitigate the vanishing gradient downside and to seize extra long-range dependencies amongst phrases.

At a sure level, we understood that the one essential factor was the eye mechanism, and your complete RNN structure was overkill. Therefore, Attention is All You Need!

Self-Consideration in Transformers

Classical consideration signifies the place phrases within the output sequence ought to focus consideration in relation to the phrases in enter sequence. That is essential in sequence-to-sequence duties like MT.

The self-attention is a selected kind of consideration. It operates between any two parts in the identical sequence. It supplies data on how “correlated” the phrases are in the identical sentence.

For a given token (or phrase) in a sequence, self-attention generates an inventory of consideration weights similar to all different tokens within the sequence. This course of is utilized to every token within the sentence, acquiring a matrix of consideration weights (as within the image).

That is the final concept, in observe issues are a bit extra sophisticated as a result of we need to add many learnable parameters to our neural community, let’s see how.

Ok, V, Q representations

Our mannequin enter is a sentence like “my title is Marcello Politi”. With the method of tokenization, a sentence is transformed into an inventory of numbers like [2, 6, 8, 3, 1].

Earlier than feeding the sentence into the transformer we have to create a dense illustration for every token.

The way to create this illustration? We multiply every token by a matrix. The matrix is discovered throughout coaching.

Let’s add some complexity now.

For every token, we create 3 vectors as an alternative of 1, we name these vectors: key, worth and question. (We see later how we create these 3 vectors).

Conceptually these 3 tokens have a selected that means:

• The vector key represents the core data captured by the token
• The vector worth captures the total data of a token
• The vector question, it’s a query concerning the token relevance for the present job.

So the concept is that we give attention to a selected token i , and we need to ask what’s the significance of the opposite tokens within the sentence relating to the token i we’re bearing in mind.

Because of this we take the vector q_i (we ask a query relating to i) for token i, and we do some mathematical operations with all the opposite tokens k_j (j!=i). That is like questioning at first look what are the opposite tokens within the sequence that look actually essential to grasp the that means of token i.

What is that this magical mathematical operation?

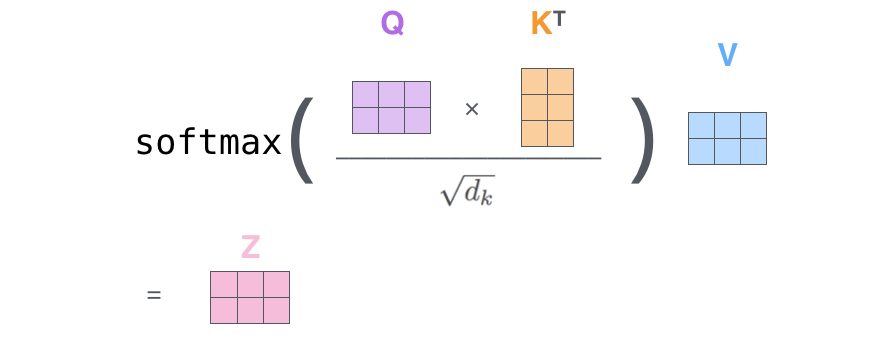
We have to multiply (dot-product) the question vector by the important thing vectors and divide by a scaling issue. We do that for every k_j token.

On this approach, we get hold of a rating for every pair (q_i, k_j). We make this listing turn out to be a chance distribution by making use of a softmax operation on it. Nice now now we have obtained the consideration weights!

With the eye weights, we all know what’s the significance of every token k_j to for undestandin the token i. So now we multiply the worth vector v_j related to every token per its weight and we sum the vectors. On this approach we get hold of the ultimate context-aware vector of token_i.

If we’re computing the contextual dense vector of token_1 we calculate:

z1 = a11*v1 + a12*v2 + … + a15*v5

The place a1j are the pc consideration weights, and v_j are the worth vectors.

Achieved! Nearly…

I didn’t cowl how we obtained the vectors okay, v and q of every token. We have to outline some matrices w_k, w_v and w_q in order that once we multiply:

• token * w_k -> okay
• token * w_q -> q
• token * w_v -> v

These 3 matrices are set at random and are discovered throughout coaching, that is why now we have many parameters in trendy fashions similar to LLMs.

Multi-head Self-Consideration in Transformers (MHSA)

Are we positive that the earlier self-attention mechanism is ready to seize all essential relationships amongst tokens (phrases) and create dense vectors of these tokens that basically make sense?

It might truly not work at all times completely. What if to mitigate the error we re-run your complete factor 2 instances with new w_q, w_k and w_v matrices and one way or the other merge the two dense vectors obtained? On this approach possibly one self-attention managed to seize some relationship and the opposite managed to seize another relationship.

Properly, that is what precisely occurs in MHSA. The case we simply mentioned incorporates two heads as a result of it has two units of w_q, w_k and w_v matrices. We will have much more heads: 4, 8, 16 and many others.

The one sophisticated factor is that each one these heads are managed in parallel, we course of the all in the identical computation utilizing tensors.

The way in which we merge the dense vectors of every head is easy, we concatenate them (therefore the dimension of every vector shall be smaller in order that when concat them we get hold of the unique dimension we needed), and we cross the obtained vector by means of one other w_o learnable matrix.

Palms-on

Suppose you’ve gotten a sentence. After tokenization, every token (phrase for simplicity) corresponds to an index (quantity):

Earlier than feeding the sentence into the transofrmer we have to create a dense illustration for every token.

The way to create these illustration? We multiply every token per a matrix. This matrix is discovered throughout coaching.

Let’s construct this embedding matrix.

If we multiply our tokenized sentence with the embeddings, we get hold of a dense illustration of dimension 16 for every token

In an effort to use the eye mechanism we have to create 3 new We outline 3 matrixes w_q, w_k and w_v. After we multiply one enter token time the w_q we get hold of the vector q. Similar with w_k and w_v.

Compute consideration weights

Let’s now compute the eye weights for less than the primary enter token of the sentence.

We have to multiply the question vector related to token1 (query_1) with all of the keys of the opposite vectors.

So now we have to compute all of the keys (key_2, key_2, key_4, key_5). However wait, we are able to compute all of those in a single time by multiplying the sentence_embed instances the w_k matrix.

Let’s do the identical factor with the values

Let’s compute the primary a part of the attions formulation.

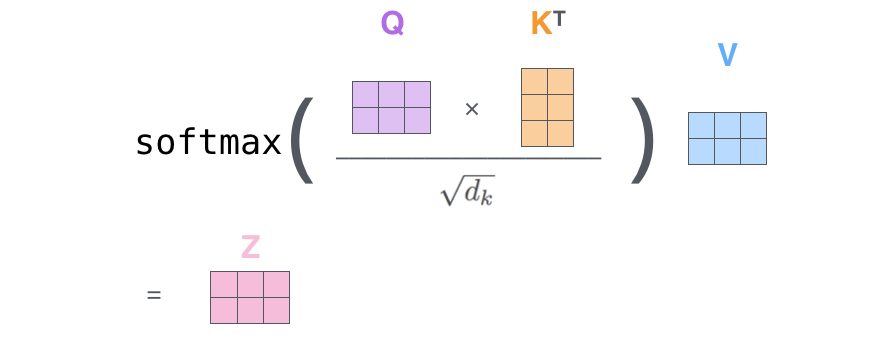
import torch.nn.purposeful as F

With the eye weights we all know what’s the significance of every token. So now we multiply the worth vector related to every token per its weight.

To acquire the ultimate context conscious vector of token_1.

In the identical approach we might compute the context conscious dense vectors of all the opposite tokens. Now we’re at all times utilizing the identical matrices w_k, w_q, w_v. We are saying that we use one head.

However we are able to have a number of triplets of matrices, so multi-head. That’s why it’s referred to as multi-head consideration.

The dense vectors of an enter tokens, given in oputut from every head are at then finish concatenated and linearly remodeled to get the ultimate dense vector.

Implementing MultiheadSelf-Consideration

Similar steps as earlier than…

We’ll outline a multi-head consideration mechanism with h heads (let’s say 4 heads for this instance). Every head may have its personal w_q, w_k, and w_v matrices, and the output of every head will likely be concatenated and handed by means of a ultimate linear layer.

Because the output of the top will likely be concatenated, and we wish a ultimate dimension of d, the dimension of every head must be d/h. Moreover every concatenated vector will go although a linear transformation, so we want one other matrix w_ouptut as you may see within the formulation.

Since now we have 4 heads, we wish 4 copies for every matrix. As an alternative of copies, we add a dimension, which is identical factor, however we solely do one operation. (Think about stacking matrices on prime of one another, its the identical factor).

I’m utilizing for simplicity torch’s einsum. Should you’re not aware of it take a look at my blog post.

The einsum operation torch.einsum('sd,hde->hse', sentence_embed, w_query) in PyTorch makes use of letters to outline the way to multiply and rearrange numbers. Right here’s what every half means:

1. Enter Tensors:
   • sentence_embed with the notation 'sd':
     • s represents the variety of phrases (sequence size), which is 5.
     • d represents the variety of numbers per phrase (embedding dimension), which is 16.
     • The form of this tensor is [5, 16].
   • w_query with the notation 'hde':
     • h represents the variety of heads, which is 4.
     • d represents the embedding dimension, which once more is 16.
     • e represents the brand new quantity dimension per head (d_k), which is 4.
     • The form of this tensor is [4, 16, 4].
2. Output Tensor:
   • The output has the notation 'hse':
     • h represents 4 heads.
     • s represents 5 phrases.
     • e represents 4 numbers per head.
     • The form of the output tensor is [4, 5, 4].

This einsum equation performs a dot product between the queries (hse) and the transposed keys (hek) to acquire scores of form [h, seq_len, seq_len], the place:

• h -> Variety of heads.
• s and okay -> Sequence size (variety of tokens).
• e -> Dimension of every head (d_k).

The division by (d_k ** 0.5) scales the scores to stabilize gradients. Softmax is then utilized to acquire consideration weights:

Now we concatenate all of the heads of token 1

Let’s lastly multiply per the final w_output matrix as within the formulation above

Remaining Ideas

On this weblog submit I’ve applied a easy model of the eye mechanism. This isn’t how it’s actually applied in trendy frameworks, however my scope is to offer some insights to permit anybody an understanding of how this works. In future articles I’ll undergo your complete implementation of a transformer structure.

Comply with me on TDS in the event you like this text! 😁

💼 Linkedin ️| 🐦 X (Twitter) | 💻 Website

Until in any other case famous, pictures are by the writer