Within the decision (ER), one of many central challenges is managing and sustaining the complicated relationships between data. At its core, Tilores fashions entities as graphs: every node represents a file, and edges symbolize rule-based matches between these data. This strategy provides us flexibility, traceability, and a excessive stage of accuracy, but it surely additionally comes with important storage and computational challenges, particularly at scale. This text explains the main points about effectively storing extremely linked graphs utilizing clique-based graph Compression.
The Entity Graph Mannequin
In Tilores, a legitimate entity is a graph the place each file is linked to a minimum of one different through an identical rule. As an example, if file a matches file b in response to rule R1, we retailer that as an edge "a:b:R1". If one other rule, say R2, additionally connects a and b, we retailer an extra edge "a:b:R2". These edges are stored as a easy listing, however might alternatively be modeled utilizing an adjacency listing construction for extra environment friendly storage.
Why Retain All Edges?
Most Entity Resolution programs or grasp information administration programs don’t retain the relationships between data, however solely retailer a illustration of the underlying information and sometimes a generic matching rating, leaving the person unsure about how the entity was shaped. Even worse, the person has no technique to right errors made by the automated matching system.
Therefore, retaining all edges in an entity graph serves a number of functions:
- Traceability: Permits the person to grasp why two data have been grouped into the identical entity.
- Analytics: Insights equivalent to rule effectiveness and information similarity could be extracted from edge metadata.
- Information Deletion & Recalculation: When a file is deleted or a rule is modified, the graph have to be recalculated. Edge data is crucial to grasp how an entity was shaped and the way it must be up to date.
The Scaling Drawback: Quadratic Progress
When discussing potential scaling points in entity decision, this sometimes refers back to the problem of matching every file with all different data. Whereas this can be a challenge on its own, retaining all edges of an entity leads to related points on the storage facet. Entities the place many data are linked with one another create a large number of edges. Within the worst case each new file is linked to all present data. This quadratic development could be expressed with the system:
n * (n - 1) / 2
For small entities, this isn’t a difficulty. For instance, an entity with 3 data can have a most of three edges. For n = 100, this will increase to 4,950 edges and for n = 1,000 this leads to as much as 499,500 edges.
This creates an immense storage and computational overhead, particularly since entity decision graphs usually exhibit this sort of dense connectivity.
Answer: Clique-Based mostly Graph Compression (CBGC)
A clique in a graph is a bunch of nodes the place each node is linked to each different node in that group. A clique may also be known as a whole subgraph. The smallest doable clique comprises a single node and no edges. A pair of nodes linked by an edge additionally varieties a clique. And three nodes, such because the one beneath, kind a triangle formed clique.
(picture by the creator)
A maximal clique is a clique that can’t be prolonged by including any adjoining node, and a most clique is the clique with the biggest variety of nodes in the entire graph. For the aim of this text, we’re going to make use of the time period clique solely to consult with cliques with a minimum of three nodes.
The beforehand proven triangle might be represented in Tilores by the next edges:
[
"a:b:R1",
"a:c:R1",
"b:c:R1"
]As a result of a triangle is a clique, we might additionally symbolize the graph by storing solely the nodes on this clique and the related rule ID:
{
"R1": [
["a", "b", "c"]
]
}Let’s take into account the next barely extra difficult graph:

(picture by the creator)
Based mostly on its look, we are able to simply spot that every one nodes are linked to one another. So as a substitute of itemizing all 15 edges [remember n*(n-1)/2], we are able to merely retailer this clique within the following kind:
{
"R1":[
["a", "b", "c", "d", "e", "f"]
]
}Nonetheless, in a sensible graph, not all data are linked to one another. Take into account the next graph:

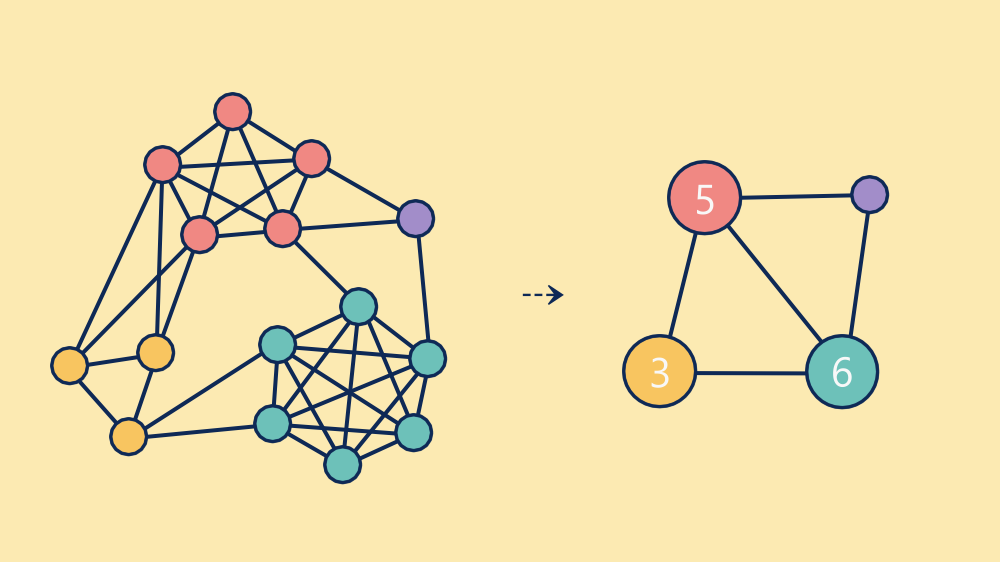
(picture by the creator)
There are three bigger cliques highlighted: yellow, crimson and blue (teal when you’re choosy). There’s additionally a single remaining node. Whereas these are in all probability the biggest cliques, you would possibly spot dozens of others. For instance, do you discover the 4-node clique between the 2 crimson and two yellow nodes?
Sticking with the coloured cliques, we might retailer them within the following method (utilizing y, r and b for yellow, crimson and blue):
{
"R1": [
["y1", "y2", "y3"],
["r1", "r2", "r3", "r4", "r5"],
["b1", "b2", "b3", "b4", "b5", "b6"]
]
}Moreover, we are able to retailer the remaining 10 edges (p for purple):
[
"y1:r1:R1",
"y1:r2:R1",
"y2:r1:R1",
"y2:r2:R1",
"r4:p1:R1",
"r5:p1:R1",
"r5:b1:R1",
"b2:p1:R1",
"y3:b5:R1",
"y3:b6:R1"
]Because of this the entire graph can now be represented with solely three cliques and ten edges, as a substitute of the unique 38 edges.

(picture by the creator)
This clique-based graph compression (CBGC) is loss-free (until you want edge properties). In a sensible dataset, we recognized huge storage financial savings. For one buyer, CBGC decreased edge storage by 99.7%, changing a whole lot of 1000’s of edges with only a few hundred cliques and sparse edges.
Efficiency Advantages Past Storage
CBGC isn’t just about compression. It additionally permits quicker operations, significantly when dealing with file and edge deletion.
Any sane entity decision engine ought to cut up an entity into a number of ones if the one hyperlink between two subgraphs was deleted, for instance, because of regulatory or compliance causes. Figuring out separate, unconnected subgraphs is usually completed utilizing a linked elements algorithm. In brief, it really works by grouping all nodes which might be linked through edges into separate subgraphs. Consequently every edge must be checked a minimum of as soon as.
Nonetheless, if a graph is saved as a compressed graph, then there is no such thing as a must traverse all edges of a clique. As an alternative it’s adequate so as to add a restricted variety of edges for every clique, for instance a transitive path between the nodes of a clique, treating every clique as a pre-connected subgraph.
Commerce-Offs: Clique Detection Complexity
There’s a trade-off: clique detection is computationally costly, significantly when looking for the utmost cliques, a widely known NP-hard drawback.
In apply it’s usually adequate to simplify this workload. Approximate algorithms for clique detection (e.g. grasping heuristics) carry out effectively sufficient for many makes use of. Moreover, CBGC is recalculated selectively, often when an entity’s edge depend surpasses a threshold. This hybrid strategy balances compression effectivity with acceptable processing price.
Past Cliques
Arguably, the commonest sample in entity decision is the entire subgraph. Nonetheless, additional optimization might be achieved by figuring out different recurring patterns equivalent to
- stars: retailer as an inventory of nodes the place the primary entry represents the central node
- paths: retailer as an ordered listing of nodes
- communities: retailer like a clique and mark the lacking edges
Closing Ideas
Entity decision programs usually face the problem of managing dense, extremely interconnected graphs. Storing all edges naively shortly turns into unsustainable. CBGC offers an environment friendly technique to mannequin entities by exploiting structural properties of the information.
Not solely does it cut back storage overhead, but it surely additionally improves system efficiency, particularly throughout information deletion and reprocessing. Whereas clique detection has its computational prices, cautious engineering decisions enable us to reap the advantages with out sacrificing scalability.