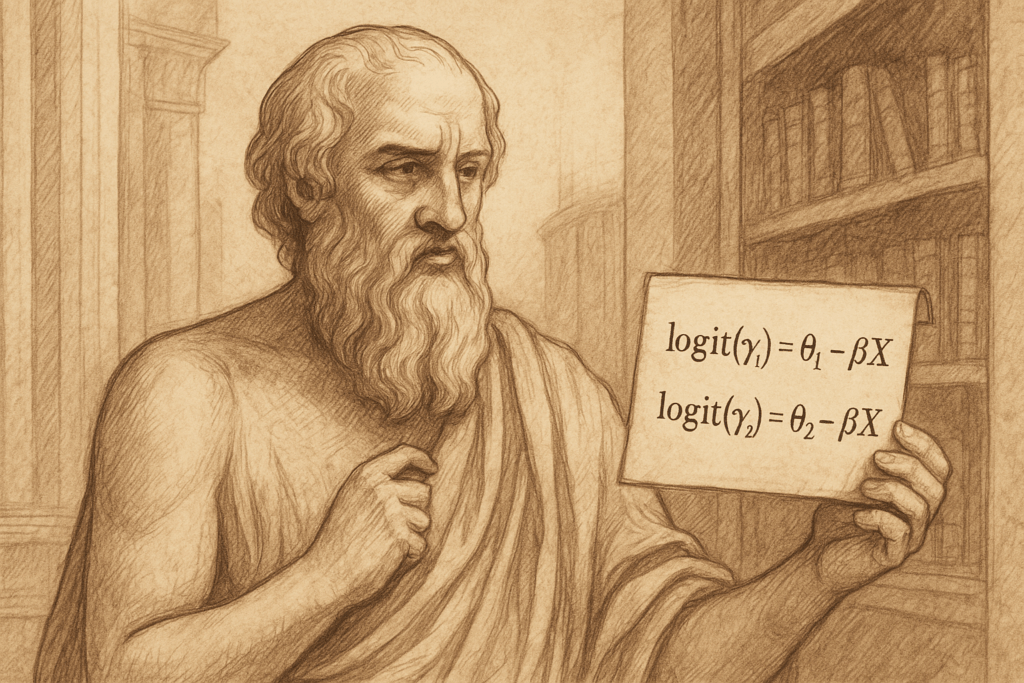Exploring the Proportional Odds Model for Ordinal Logistic Regression

You could find the total code for this instance on the backside of this publish.

odds mannequin for ordinal logistic regression was first launched by McCullagh (1980). This mannequin extends binary logistic regression to conditions the place the dependent variable is ordinal [it consists of ordered categorical values]. The proportional odds mannequin is constructed on a number of assumptions, together with independence of observations, linearity of the log-odds, absence of multicolinearity amongst predictors, and the proportional odds assumption. This final assumption states that the regression coefficients are fixed throughout all thresholds of the ordinal dependent variable. Guaranteeing the proportional odds assumption holds is essential for the validity and interpretability of the mannequin.

A wide range of strategies have been proposed within the literature to evaluate mannequin match and, particularly, to check the proportional odds assumption. On this paper, we give attention to two approaches developed by Brant in his article Brant (1990), “Assessing Proportionality within the Proportional Odds Mannequin for Ordinal Logistic Regression.” We additionally show easy methods to implement these methods in Python, making use of them to real-world knowledge. Whether or not you come from a background in knowledge science, machine studying, or statistics, this text goals to assist your perceive easy methods to consider mannequin slot in ordinal logistic regression.

This paper is organized into 4 foremost sections:

1. The primary part introduces the proportional odds mannequin and its assumptions.
2. The second part discusses easy methods to assess the proportional odds assumption utilizing the probability ratio check.
3. The third part covers the evaluation of the proportional odds assumption utilizing the separate matches method.
4. The ultimate part gives examples, illustrating the implementation of those evaluation strategies in Python with knowledge.

1. Introduction to the Proportional Odds Mannequin

Earlier than presenting the mannequin, we introduce the info construction. We assume we have now N unbiased observations. Every remark is represented by a vector of p explanatory variables X_i = (X_i1, X_i2, …, X_ip), together with a dependent or response variable Y that takes ordinal values from 1 to Okay. The proportional odds mannequin particularly fashions the cumulative distribution chances of the response variable Y, outlined as γ_j = P(Y ≤ j | X_i) for j = 1, 2, …, Okay – 1, as capabilities of the explanatory variables X_i. The mannequin is formulated as follows:

logit(γⱼ) = log(γⱼ / (1 − γⱼ)) = θⱼ − βᵀ𝐗. (1)

The place θⱼ are the intercepts for every class j and respect the situation θ₁ We observe a monotonic pattern within the coefficients θⱼ throughout the classes of the response variable Y.

This mannequin is also referred to as the grouped steady mannequin, as it may be derived by assuming the existence of a steady latent variable Y∗. This latent variable follows a linear regression mannequin with conditional imply η = βᵀ𝐗, and it pertains to the noticed ordinal variable Y via thresholds θⱼ outlined as follows:

       y∗ = βᵀ𝐗+ϵ,         (2)

the place ϵ is an error time period (random noise), typically assumed to observe a normal logistic distribution within the proportional odds mannequin.

The latent variable Y^* is unobserved and partitioned into intervals outlined by thresholds θ₁, θ₂, …, θₖ₋₁, producing the noticed ordinal variable Y as follows:        

Within the subsequent part, we introduce the varied approaches proposed by Brant (1990) for assessing the proportional odds assumption. These strategies consider whether or not the regression coefficients stay fixed throughout the classes outlined by the ordinal response variable.

2. Assessing the Proportional Odds Assumption: The Probability Ratio Check

To evaluate the proportional odds assumption in an ordinal logistic regression mannequin, Brant (1990) proposes the usage of the probability ratio check. This method begins by becoming a much less restrictive mannequin through which the regression coefficients are allowed to range throughout classes. This mannequin is expressed as:

logit(γ_j) = θ_j − β_j^T𝐗. for j = 1, …, Okay-1 (4)

the place β_j is the vector [vector of dimension p] of regression coefficients for every class j. Right here the coefficients β_j are allowed to range throughout classes, which implies that the proportional odds assumption isn’t glad. We then use the conventionnel probability ratio check to evaluate the speculation :

H₀ : β_j = β for all j = 1, 2, …, Okay−1. (5)

To carry out this check, we conduct a probability ratio check evaluating the unconstrained (non-proportional or satured) mannequin with the constrained (proportional odds or decreased) mannequin.

Earlier than continuing additional, we briefly recall easy methods to use the probability ratio check in speculation testing. Suppose we need to consider the null speculation H₀ : θ ∈ Θ₀ towards the choice H₁ : θ ∈ Θ₁,

The probability ratio statistic is outlined as:

the place 𝓛(θ) is the probability operate, θ̂ is the utmost probability estimate (MLE) underneath the total mannequin, and θ̂₀ is the MLE underneath the constrained mannequin. The check statistic λ follows a chi-square distribution with levels of freedom equal to the distinction within the variety of parameters between the total and constrained fashions.

Right here, θ̂ is the utmost probability estimate (MLE) underneath the total (unconstrained) mannequin, and θ̂₀ is the MLE underneath the constrained mannequin the place the proportional odds assumption holds. The
check statistic λ follows a chi-square distribution underneath the null speculation.

In a basic setting, suppose the total parameter area is denoted by

     Θ = (θ₁, θ₂, …, θ_q, …, θ_p),

and the restricted parameter area underneath the null speculation is

     Θ₀ = (θ₁, θ₂, …, θ_q).

(Word: These parameters are generic and shouldn’t be confused with the Okay−1 thresholds or intercepts within the proportional odds mannequin.), the probability ratio check statistic λ follows a chi-square distribution with p−q levels of freedom. The place p represents the overall variety of parameters within the full (unconstrained or “saturated”) mannequin, whereas Okay−1 corresponds to the variety of parameters within the decreased (restricted) mannequin.

Now, allow us to apply this method to the ordinal logistic regression mannequin with the proportional odds assumption. Assume that our response variable has Okay ordered classes and that we have now p predictor variables. To make use of the probability ratio check to guage the proportional odds assumption, we have to examine two fashions:

1. Unconstrained Mannequin (non-proportional odds):

This model allows each outcome threshold to have its own set of regression coefficients, meaning that we do not assume the regression coefficients are equal across all thresholds. The model is defined as:

logit(γ_j) = θ_j − β_j^T𝐗. for j = 1, …, K-1 (7)

• There are K−1 threshold (intercept) parameters: θ₁, θ₂, … , θ_K-1
• Each threshold has its own vector of slope coefficients β_j of dimension p

Thus, the total number of parameters in the unconstrained model is:

(K−1) thresholds + (K−1)×p slopes = (K−1)(p+1).

2. Proportional Odds Model:

This model assumes a single set of regression coefficients for all thresholds:

logit(γ_j) = θ_j − β^T𝐗. for j = 1, …, K-1 (8)

• There are K−1 threshold parameters
• There is one common slope vector β (of dimension p x 1) for all j

Thus, the total number of parameters in the proportional odds model is:

(K−1) thresholds+p slopes=(K−1)+p

Thus, the likelihood ratio test statistic follows a chi-square distribution with degrees of freedom:

df = [(K−1)×(p+1)]−[(K−1)+p] = (K−2)×p

This test provides a formal way to assess whether the proportional odds assumption holds for the given data. At a significance level of 1%, 5%, or any other conventional threshold, the proportional odds assumption is rejected if the test statistic λ exceeds the critical value from the chi-square distribution with (K−2)×p degrees of freedom.

In other words, we reject the null hypothesis

H₀ : β₁ = β₂ = ⋯ =β_K-1 = β,

which states that the regression coefficients are equal across all cumulative logits. This test has the advantage of being straightforward to implement and provides an overall assessment of the proportional odds assumption.

In the next section, we introduce the proportional odds test based on separate fits.

3. Assessing the Proportional Odds Assumption: The Separate Fits Approach.

To understand this section, it’s important first to understand the concept and properties of the Mahalanobis distance. This distance is used to quantify how different two vectors are in a multivariate space that shares the same distribution.

Let x = (x₁, x₂, …, xₚ)ᵀ and y = (y₁, y₂, …, yₚ)ᵀ. The Mahalanobis distance between them is defined as:

where Σ is the covariance matrix of the distribution. The Mahalanobis distance squared is closely related to the chi-squared (χ²) distribution. Specifically, if X ∼ N(μ, Σ) is a p-dimensional normally distributed random vector with mean μ and covariance matrix Σ, then the Mahalanobis distance Dₘ(X, μ)² follows a χ² distribution with p degrees of freedom.

Understanding this relationship is crucial for evaluating proportionality using separate model fits — a topic we will return to shortly.

In fact, the author notes that the natural approach to evaluating the proportional odds assumption is to fit a set of K−1 binary logistic regression models (where K is the number of categories of the response variable), and then use the statistical properties of the estimated parameters to construct a test statistic for the proportional odds hypothesis.

The procedure is as follows:

First, we construct separate binary logistic regression models for each threshold j = 1, 2, …, K−1 of the ordinal response variable Y. For each threshold j, we define a binary variable Z_j, which takes the value 1 if the observation exceeds threshold j, and 0 otherwise. Specifically, we have:

With the probability, π_j = P(Z_j = 1 | X) = 1−γ_j satisfying the logistic regression model:

logit(π_j ) = θ_j − β^T𝐗. for j = 1, …, K-1 (10)

Then, assessing the proportional odds assumption in this context involves testing the hypothesis that the regression coefficients β_j are equal across all K−1 models. This is equivalent to testing the hypothesis:

H₀ : β₁ = β₂ = ⋯ = β_K-1 (11)

Let β̂ⱼ denote the maximum likelihood estimators of the regression coefficients for each binary model, and let β̂ = (β̂₁ᵀ, β̂₂ᵀ, …, β̂ₖ₋₁ᵀ)ᵀ represent the global vector of estimators. This vector is asymptotically normally distributed, such that 𝔼(β̂ⱼ) ≈ β, with variance-covariance matrix 𝕍(β̂ⱼ). The general term of this matrix, cov(β̂ⱼ, β̂ₖ), needs to be determined and is given by:

where Cov(β̂ⱼ, β̂ₖ) is the covariance between the estimated coefficients of the j-th and k-th binary models. The asymptotic covariances, Cov(β̂ⱼ, β̂ₖ), are obtained by deleting the first row and column of:

(X₊^T W_jj X₊)^-1X₊^TW_jlX₊ (Xᵗ W_llX₊)^-1

where W_jl: n × n is diagonal with typical entry π_l − π_j π_l for j ≤ l, and X₊: n x p matrix denotes the matrix of explanatory variables augmented on the left with a column of ones [1’s].

To evaluate the proportional odds assumption, Brant constructs a matrix 𝐃 that captures the differences between the coefficients β̂ⱼ. Recall that each vector β̂ⱼ has dimension p. The matrix 𝐃 is defined as follows:

where 𝐈 is the identity matrix of size p × p. The first row of the matrix 𝐃 corresponds to the difference between the first and second coefficients, the second row corresponds to the difference between the second and third coefficients, and so on, until the last row which corresponds to the difference between the (K − 2)-th and (K − 1)-th coefficients. We can notice that the product 𝐃β̂ will yield a vector of differences between the coefficients β̂ⱼ.

Once the matrix 𝐃 is constructed, Brant defines the Wald statistic X² to test the proportional odds assumption. This statistic can be interpreted as the Mahalanobis distance between the vector 𝐃β̂ and the zero vector. The Wald statistic is defined as follows:

which will be asymptotically χ² distributed with (K − 2)p degrees of freedom under the null hypothesis. The challenging part here is to determine the variance-covariance matrix 𝕍̂(β̂). In his article, Brant provides an explicit estimator for this variance-covariance matrix, which is based on the maximum likelihood estimators β̂ⱼ from each binary model.

In the following sections, we implement these approaches in Python, using the statsmodels package for the regressions and statistical tests.

Example: Application of the Two Proportional Odds Tests

The data for this example comes from the “Wine Quality” dataset, which contains information about red wine samples and their quality ratings. The dataset includes 1,599 observations and 12 variables. The target variable, “quality,” is ordinal and originally ranges from 3 to 8. To ensure enough observations in each group, we combine categories 3 and 4 into a single category (labeled 4), and categories 7 and 8 into a single category (labeled 7), so the response variable has four levels. We then handle outliers in the explanatory variables using the Interquartile Range (IQR) method. Finally, we select three predictors—volatile acidity, free sulfur dioxide, and total sulfur dioxide—to use in our ordinal logistic regression model, and we standardize these variables to have a mean of 0 and a standard deviation of 1.

Tables 1 and 2 below present the results of the three binary logistic regression models and the proportional odds model, respectively. Several discrepancies can be seen in these tables, particularly in the “volatile acidity” coefficients. For instance, the difference in the “volatile acidity” coefficient between the first and second binary models is -0.280, while the difference between the second and third models is 0.361. These differences suggest that the proportional odds assumption may not hold [I also suggest to compute standard errors of difference for more confidence].

To assess the overall significance of the proportional odds assumption, we perform the likelihood ratio test, which yields a test statistic of LR = 53.207 and a p-value of 1.066 × 10^-9 when compared to the chi-square distribution with 6 degrees of freedom. This result indicates that the proportional odds assumption is violated at the 5% significance level, suggesting that the model may not be appropriate for the data. We also use the separate fits approach to further investigate this assumption. The Wald test statistic is computed as X² = 41.880, with a p-value of 1.232 × 10^-7, also based on the chi-square distribution with 6 degrees of freedom. This further confirms that the proportional odds assumption is violated at the 5% significance level.

Conclusion

This paper had two main goals: first, to illustrate how to test the proportional odds assumption in the context of ordinal logistic regression, and second, to encourage readers to explore Brant (1990)’s article for a deeper understanding of the subject.

Brant’s work extends past assessing the proportional odds assumption—it additionally gives strategies for evaluating the general adequacy of the ordinal logistic regression mannequin. For example, he discusses easy methods to check whether or not the latent variable Y∗ actually follows a logistic distribution or whether or not an alternate hyperlink operate is likely to be extra acceptable.

On this article, we centered on a world evaluation of the proportional odds assumption, with out investigating which particular coefficients could also be chargeable for any violations. Brant additionally addresses this finer-grained evaluation, which is why we strongly encourage you to learn his article in full.

Picture Credit

All photos and visualizations on this article had been created by the writer utilizing Python (pandas, matplotlib, seaborn, and plotly) and excel, except in any other case acknowledged.

References

Brant, Rollin. 1990. “Assessing Proportionality within the Proportional Odds Mannequin for Ordinal Logistic Regression.” Biometrics, 1171–78.

McCullagh, Peter. 1980. “Regression Fashions for Ordinal Knowledge.” Journal of the Royal Statistical Society: Collection B (Methodological) 42 (2): 109–27.

Wasserman, L. (2013). All of statistics: a concise course in statistical inference. Springer Science & Enterprise Media.

Cortez, P., Cerdeira, A., Almeida, F., Matos, T., & Reis, J. (2009). Wine High quality [Dataset]. UCI Machine Studying Repository. https://doi.org/10.24432/C56S3T.

Knowledge & Licensing

The dataset used on this article is licensed underneath the Inventive Commons Attribution 4.0 Worldwide (CC BY 4.0) license.

It permits to be used, distribution, and adaptation, even for business functions, offered that acceptable credit score is given.

The unique dataset was printed by [Name of the Author / Institution] and is accessible here.

Codes

Import knowledge and the variety of observations

import pandas as pd

knowledge = pd.read_csv("winequality-red.csv", sep=";")
knowledge.head()

# Repartition de la variable cible high quality 

knowledge['quality'].value_counts(normalize=False).sort_index()

# I need to regroup modalities 3, 4 and the modalities 7 and eight
knowledge['quality'] = knowledge['quality'].exchange({3: 4, 8: 7})
knowledge['quality'].value_counts(normalize=False).sort_index()
print("Variety of observations:", knowledge.form[0])

Let’s deal with the outliers of the predictor variables (excluding the goal variable high quality) utilizing the IQR methodology.

def remove_outliers_iqr(df, column):
    Q1 = df[column].quantile(0.25)
    Q3 = df[column].quantile(0.75)
    IQR = Q3 - Q1
    lower_bound = Q1 - 1.5 * IQR
    upper_bound = Q3 + 1.5 * IQR
    return df[(df[column] >= lower_bound) & (df[column] 

Create a boxplot of every variable per group of high quality

var_names_without_quality = [col for col in data.columns if col != 'quality']

##  Create the boxplot of every variable per group of high quality
import matplotlib.pyplot as plt
import seaborn as sns
plt.determine(figsize=(15, 10))
for i, var in enumerate(var_names_without_quality):
    plt.subplot(3, 4, i + 1)
    sns.boxplot(x='high quality', y=var, knowledge=knowledge)
    plt.title(f'Boxplot of {var} by high quality')
    plt.xlabel('High quality')
    plt.ylabel(var)
plt.tight_layout()
plt.present()

Implement Ordinal regression for the odd proportionality check.

# Implement the ordered logistic regression to variables 'risky acidity', 'free sulfur dioxide', and 'whole sulfur dioxide'
from statsmodels.miscmodels.ordinal_model import OrderedModel
from sklearn.preprocessing import StandardScaler
explanatory_vars = ['volatile acidity', 'free sulfur dioxide', 'total sulfur dioxide']
# Standardize the explanatory variables
knowledge[explanatory_vars] = StandardScaler().fit_transform(knowledge[explanatory_vars])

def fit_ordered_logistic_regression(knowledge, response_var, explanatory_vars):
    mannequin = OrderedModel(
        knowledge[response_var],
        knowledge[explanatory_vars],
        distr='logit'
    )
    end result = mannequin.match(methodology='bfgs', disp=False)
    return end result
response_var = 'high quality'

end result = fit_ordered_logistic_regression(knowledge, response_var, explanatory_vars)
print(end result.abstract())
# Compute the log-likelihood of the mannequin
log_reduced = end result.llf
print(f"Log-likelihood of the decreased mannequin: {log_reduced}")

Compute the total multinomial mannequin

# The probability ratio check
# Compute the total multinomial mannequin
import statsmodels.api as sm

data_sm = sm.add_constant(knowledge[explanatory_vars])
model_full = sm.MNLogit(knowledge[response_var], data_sm)
result_full = model_full.match(methodology='bfgs', disp=False)
#abstract
print(result_full.abstract())
# Commpute the log-likelihood of the total mannequin
log_full = result_full.llf
print(f"Log-likelihood of the total mannequin: {log_full}")

# Compute the probability ratio statistic

LR_statistic = 2 * (log_full - log_reduced)
print(f"Probability Ratio Statistic: {LR_statistic}")

# Compute the levels of freedom
df1 = (num_of_thresholds - 1) * len(explanatory_vars)
df2 = result_full.df_model - OrderedModel(
        knowledge[response_var],
        knowledge[explanatory_vars],
        distr='logit'
    ).match().df_model
print(f"Levels of Freedom: {df1}")
print(f"Levels of Freedom for the total mannequin: {df2}")

# Compute the p-value
from scipy.stats import chi2
print("The LR statistic :", LR_statistic)
p_value = chi2.sf(LR_statistic, df1)
print(f"P-value: {p_value}")
if p_value 

The code beneath constructs the Wald statistic X² = (𝐃β̂)ᵀ [𝐃𝕍̂(β̂)𝐃ᵀ]⁻¹ (𝐃β̂)

Okay-1 Binary Logit Estimation for Proportional Odds Assumption Test

import numpy as np
import statsmodels.api as sm
import pandas as pd

def fit_binary_models(knowledge, explanatory_vars, y):
    """
    Matches a sequence of binary logistic regression fashions to evaluate the proportional odds assumption.

    Parameters:
    - knowledge: Authentic pandas DataFrame (should embody all variables)
    - explanatory_vars: Record of predictor variables (options)
    - y: Array-like ordinal goal variable (n,) — e.g., classes like 4, 5, 6, 7

    Returns:
    - binary_models: Record of fitted binary Logit mannequin objects (statsmodels)
    - beta_hat: (Okay−1) × (p+1) array of estimated coefficients (together with intercept)
    - var_hat: Record of (p+1) × (p+1) variance-covariance matrices for every mannequin
    - z_mat: DataFrame containing the binary remodeled targets z_j (for inspection/debugging)
    - thresholds: Record of thresholds used to create the binary fashions
    """
    qualities = np.type(np.distinctive(y))           # Sorted distinctive classes of y
    thresholds = qualities[:-1]                 # Thresholds to outline binary fashions (Okay−1)
    p = len(explanatory_vars)
    n = len(y)
    K_1 = len(thresholds)

    binary_models = []
    beta_hat = np.full((K_1, p+1), np.nan)      # To retailer estimated coefficients
    p_values_beta_hat = np.full((K_1, p+1), np.nan)  # To retailer p-values
    var_hat = []
    z_mat = pd.DataFrame(index=np.arange(n))   # For storing binary goal variations
    X_with_const = sm.add_constant(knowledge[explanatory_vars])  # Design matrix with intercept

    # Match one binary logistic regression for every threshold
    for j, t in enumerate(thresholds):
        z_j = (y > t).astype(int)               # Binary goal: 1 if y > t, else 0
        z_mat[f'z>{t}'] = z_j
        mannequin = sm.Logit(z_j, X_with_const)
        res = mannequin.match(disp=0)
        binary_models.append(res)
        beta_hat[j, :] = res.params.values      # Retailer coefficients (with intercept)
        p_values_beta_hat[j, :] = res.pvalues.values
        var_hat.append(res.cov_params().values) # Retailer full (p+1) × (p+1) covariance matrix

    return binary_models, beta_hat, X_with_const, var_hat, z_mat, thresholds

# Apply the operate to the info
binary_models, beta_hat, X_with_const, var_hat, z_mat, thresholds = fit_binary_models(
    knowledge, explanatory_vars, knowledge[response_var]
)

# Show the estimated coefficients
print("Estimated coefficients (beta_hat):")
print(beta_hat)

# Show the design matrix (predictors with intercept)
print("Design matrix X (with fixed):")
print(X_with_const)

# Show the thresholds used to outline the binary fashions
print("Thresholds:")
print(thresholds)

# Show first few rows of the binary response matrix
print("z_mat (created binary goal variables):")
print(z_mat.head())

Compute Fitted Chances (π̂) for establishing the W_jl n x n diagonal matrix.

def compute_pi_hat(binary_models, X_with_const):
    """
    Computes the fitted chances π̂ for every binary logistic regression mannequin.

    Parameters:
    - binary_models: Record of fitted Logit mannequin outcomes (from statsmodels)
    - X_with_const : 2D array of form (n, p+1) — the design matrix with intercept included

    Returns:
    - pi_hat: 2D array of form (n, Okay−1) containing the anticipated chances
              from every of the Okay−1 binary fashions
    """
    n = X_with_const.form[0]           # Variety of observations
    K_1 = len(binary_models)            # Variety of binary fashions (Okay−1)
    pi_hat = np.full((n, K_1), np.nan)  # Initialize prediction matrix

    # Compute fitted chances for every binary mannequin
    for m, mannequin in enumerate(binary_models):
        pi_hat[:, m] = mannequin.predict(X_with_const)

    return pi_hat

# Assuming you have already got:
# - binary_models: listing of fitted fashions from earlier operate
# - X_with_const: design matrix with intercept (n, p+1)

pi_hat = compute_pi_hat(binary_models, X_with_const)

# Show the form and a preview of the anticipated chances matrix
print("Form of pi_hat:", pi_hat.form)      # Anticipated form: (n, Okay−1)
print("Preview of pi_hat:n", pi_hat[:5, :]) # First 5 rows

Compute the general estimated covariance matrix V̂(β̃) in two steps.

import numpy as np

# Assemble International Variance-Covariance Matrix for Slope Coefficients (Excluding Intercept)
def assemble_varBeta(pi_hat, X_with_const):
    """
    Constructs the worldwide variance-covariance matrix (varBeta) for the slope coefficients
    estimated from a sequence of binary logistic regressions.

    Parameters:
    - pi_hat        : Array of form (n, Okay−1), fitted chances for every binary mannequin
    - X_with_const  : Array of form (n, p+1), design matrix together with intercept

    Returns:
    - varBeta : Array of form ((Okay−1)*p, (Okay−1)*p), block matrix of variances and covariances
                throughout binary fashions (intercept excluded)
    """
    # Guarantee enter is a NumPy array
    X = X_with_const.values if hasattr(X_with_const, 'values') else np.asarray(X_with_const)
    n, p1 = X.form               # p1 = p + 1 (together with intercept)
    p = p1 - 1
    K_1 = pi_hat.form[1]

    # Initialize world variance-covariance matrix
    varBeta = np.zeros((K_1 * p, K_1 * p))

    for j in vary(K_1):
        pi_j = pi_hat[:, j]
        Wj = np.diag(pi_j * (1 - pi_j))         # Diagonal weight matrix for mannequin j
        XtWjX_inv = np.linalg.pinv(X.T @ Wj @ X)

        # Take away intercept (exclude first row/column)
        var_block_diag = XtWjX_inv[1:, 1:]
        row_start = j * p
        row_end = (j + 1) * p
        varBeta[row_start:row_end, row_start:row_end] = var_block_diag

        for l in vary(j + 1, K_1):
            pi_l = pi_hat[:, l]
            Wml = np.diag(pi_l - pi_j * pi_l)
            Wl = np.diag(pi_l * (1 - pi_l))
            XtWlX_inv = np.linalg.pinv(X.T @ Wl @ X)

            # Compute off-diagonal block
            block_cov = (XtWjX_inv @ (X.T @ Wml @ X) @ XtWlX_inv)[1:, 1:]

            col_start = l * p
            col_end = (l + 1) * p

            # Fill symmetric blocks
            varBeta[row_start:row_end, col_start:col_end] = block_cov
            varBeta[col_start:col_end, row_start:row_end] = block_cov.T

    return varBeta

# Compute the worldwide variance-covariance matrix
varBeta = assemble_varBeta(pi_hat, X_with_const)

# Show form and preview
print("Form of varBeta:", varBeta.form)       # Anticipated: ((Okay−1) * p, (Okay−1) * p)
print("Preview of varBeta:n", varBeta[:5, :5]) # Show top-left nook

# Fill Diagonal Blocks of the International Variance-Covariance Matrix (Excluding Intercept)
def fill_varBeta_diagonal(varBeta, var_hat):
    """
    Fills the diagonal blocks of the worldwide variance-covariance matrix varBeta utilizing
    the person covariance matrices from every binary mannequin (excluding intercept phrases).

    Parameters:
    - varBeta : International variance-covariance matrix of form ((Okay−1)*p, (Okay−1)*p)
    - var_hat : Record of (p+1 × p+1) variance-covariance matrices (together with intercept)

    Returns:
    - varBeta : Up to date matrix with diagonal blocks crammed (intercept eliminated)
    """
    K_1 = len(var_hat)                        # Variety of binary fashions
    p = var_hat[0].form[0] - 1               # Variety of predictors (excluding intercept)

    for m in vary(K_1):
        block = var_hat[m][1:, 1:]            # Take away intercept from variance block
        row_start = m * p
        row_end = (m + 1) * p
        varBeta[row_start:row_end, row_start:row_end] = block

    return varBeta

# Flatten the slope coefficients (excluding intercept) into betaStar
betaStar = beta_hat[:, 1:].flatten()

# Fill the diagonal blocks of the worldwide variance-covariance matrix
varBeta = fill_varBeta_diagonal(varBeta, var_hat)

# Output diagnostics
print("Form of varBeta after diagonal fill:", varBeta.form)           # Anticipated: ((Okay−1)*p, (Okay−1)*p)
print("Preview of varBeta after diagonal fill:n", varBeta[:5, :5])     # Prime-left preview

Building of the (okay – 2)p x (okay – I)p distinction matrix.

import numpy as np

def construct_D(K_1, p):
    """
    Constructs the distinction matrix D of form ((Okay−2)*p, (Okay−1)*p) used within the Wald check
    for assessing the proportional odds assumption in ordinal logistic regression.

    Parameters:
    - K_1 : int — variety of binary fashions, i.e., Okay−1 thresholds
    - p   : int — variety of explanatory variables (excluding intercept)

    Returns:
    - D   : numpy array of form ((Okay−2)*p, (Okay−1)*p), encoding variations between
            successive β_j slope vectors (excluding intercepts)
    """
    D = np.zeros(((K_1 - 1) * p, K_1 * p))  # Initialize D matrix
    I = np.eye(p)                          # Identification matrix for block insertion

    # Fill every row block with I and -I at acceptable positions
    for i in vary(K_1 - 1):               # i = 0 to (Okay−2)
        for j in vary(K_1):               # j = 0 to (Okay−1)
            if j == i:
                temp = I                   # Constructive id block
            elif j == i + 1:
                temp = -I                  # Detrimental id block
            else:
                temp = np.zeros((p, p))    # Zero block in any other case

            row_start = i * p
            row_end = (i + 1) * p
            col_start = j * p
            col_end = (j + 1) * p

            D[row_start:row_end, col_start:col_end] += temp

    return D

# Assemble and examine D
D = construct_D(len(thresholds), len(explanatory_vars))
print("Form of D:", D.form)            # Anticipated: ((Okay−2)*p, (Okay−1)*p)
print("Preview of D:n", D[:5, :5])      # Prime-left nook of D

Compute the Wald Statistic for Testing the Proportional Odds Assumption

def wald_statistic(D, betaStar, varBeta):
    """
    Computes the Wald chi-square statistic X² to check the proportional odds assumption.

    Parameters:
    - D         : (Okay−2)p × (Okay−1)p matrix that encodes linear contrasts between slope coefficients
    - betaStar  : Flattened vector of estimated slopes (excluding intercepts), form ((Okay−1)*p,)
    - varBeta   : International variance-covariance matrix of form ((Okay−1)*p, (Okay−1)*p)

    Returns:
    - X2        : Wald check statistic (scalar)
    """
    Db = D @ betaStar                   # Linear contrasts of beta coefficients
    V = D @ varBeta @ D.T              # Variance of the contrasts
    inv_V = np.linalg.inv(V)           # Pseudo-inverse ensures numerical stability
    X2 = float(Db.T @ inv_V @ Db)      # Wald statistic

    return X2

# Assumptions:
K_1 = len(binary_models)               # Variety of binary fashions (Okay−1)
p = len(explanatory_vars)             # Variety of explanatory variables (excluding intercept)

# Assemble distinction matrix D
D = construct_D(K_1, p)

# Compute the Wald statistic
X2 = wald_statistic(D, betaStar, varBeta)

# Levels of freedom: (Okay−2) × p
ddl = (K_1 - 1) * p

# Compute the p-value from the chi-square distribution
from scipy.stats import chi2
pval = 1 - chi2.cdf(X2, ddl)

# Output outcomes
print(f"Wald statistic X² = {X2:.4f}")
print(f"Levels of freedom = {ddl}")
print(f"p-value = {pval:.4g}")