mechanics is a approach to describe how bodily methods, like planets or pendulums, transfer over time, specializing in power moderately than simply forces. By reframing complicated dynamics by means of power lenses, this Nineteenth-century physics framework now powers cutting-edge generative AI. It makes use of generalized coordinates ( q ) (like place) and their conjugate momenta ( p ) (associated to momentum), forming a section house that captures the system’s state. This strategy is especially helpful for complicated methods with many elements, making it simpler to seek out patterns and conservation legal guidelines.
Desk of Contents
Mathematical Reformation: From Second-Order to First Order ⚙️
Newton’s ( F = mddot{q} ) requires fixing second-order differential equations, which turn out to be unwieldy for constrained methods or when figuring out conserved portions.
The Core Concept
Hamiltonian mechanics splits ( ddot{q} = F(q)/m ) into two first-order equations by introducing conjugate momentum ( p ):
[
begin{align*}
dot{q} = frac{partial H}{partial p} & text{(Position)}, quad dot{p} = -frac{partial H}{partial q} & text{(Momentum)}
end{align*}
]
It decomposes acceleration into complementary momentum/place flows. This section house perspective reveals hidden geometric construction.
Lagrangian Prelude: Motion Rules
The Lagrangian ( mathcal{L}(q, dot{q}) = Ok – U ) results in Euler-Lagrange equations through variational calculus:
[
frac{d}{dt}left( frac{partial mathcal{L}}{partial dot{q}} right) – frac{partial mathcal{L}}{partial q} = 0
]
Kinetic Vitality Image
Word that the ( Ok ) within the ( mathcal{L}(q, dot{q}) = Ok – U ) can also be represented as ( T ).
However these stay second-order. The essential leap comes by means of Legendre Transformation ( (dot{q} rightarrow p) ). The Hamiltonian is derived from the Lagrangian by means of a Legendre transformation by defining the conjugate momentum as ( p_i = frac{partial mathcal{L}}{partial dot{q}_i} ); then the Hamiltonian could be written as:
[
H(q,p) = sum_i p_i dot{q}_i – mathcal{L}(q, dot{q})
]
We are able to write ( H(q,p) ) extra intuitively as:
[
H(q,p) = K(p) + U(q)
]
This flips the script: as a substitute of ( dot{q} )-centric dynamics, we get symplectic section circulation.
Why This Issues
The Hamiltonian turns into the system’s whole power ( H = Ok + U ) for a lot of bodily methods. It additionally offers a framework the place time evolution is a canonical transformation – a symmetry preserving the basic Poisson bracket construction ( {q_i, p_j} = delta_{ij} ).
For extra about canonical, non-canonical transformations, and Poisson bracket, together with detailed math and examples, take a look at the TorchEBM post on Hamiltonian mechanics.
This transformation just isn’t canonical as a result of it doesn’t protect the Poisson bracket construction.
Newton vs. Lagrange vs. Hamilton: A Philosophical Showdown
| Facet | Newtonian | Lagrangian | Hamiltonian |
|---|---|---|---|
| State Variables | Place ( x ) and velocity ( dot{x} ) | Generalized coordinates ( q ) and velocities ( dot{q} ) | Generalized coordinates ( q ) and conjugate momenta ( p ) |
| Formulation | Second-order differential equations ( (F=ma) ) | Precept of least motion (( delta int L , dt = 0 )): ( L = Ok – U ) | First-order differential equations from Hamiltonian perform (Section circulation ( (dH) )): ( H = Ok + U ) |
| Figuring out Symmetries | Handbook identification or by means of particular strategies | Noether’s theorem | Canonical transformations and Poisson brackets |
| Machine Studying Connection | Physics-informed neural networks, simulations | Optimum management, reinforcement studying | Hamiltonian Monte Carlo (HMC) sampling, energy-based fashions |
| Vitality Conservation | Not inherent (should be derived) | Constructed-in by means of conservation legal guidelines | Central (Hamiltonian is power) |
| Basic Coordinates | Attainable, however typically cumbersome | Pure match | Pure match |
| Time Reversibility | Sure | Sure | Sure, particularly in symplectic formulations |
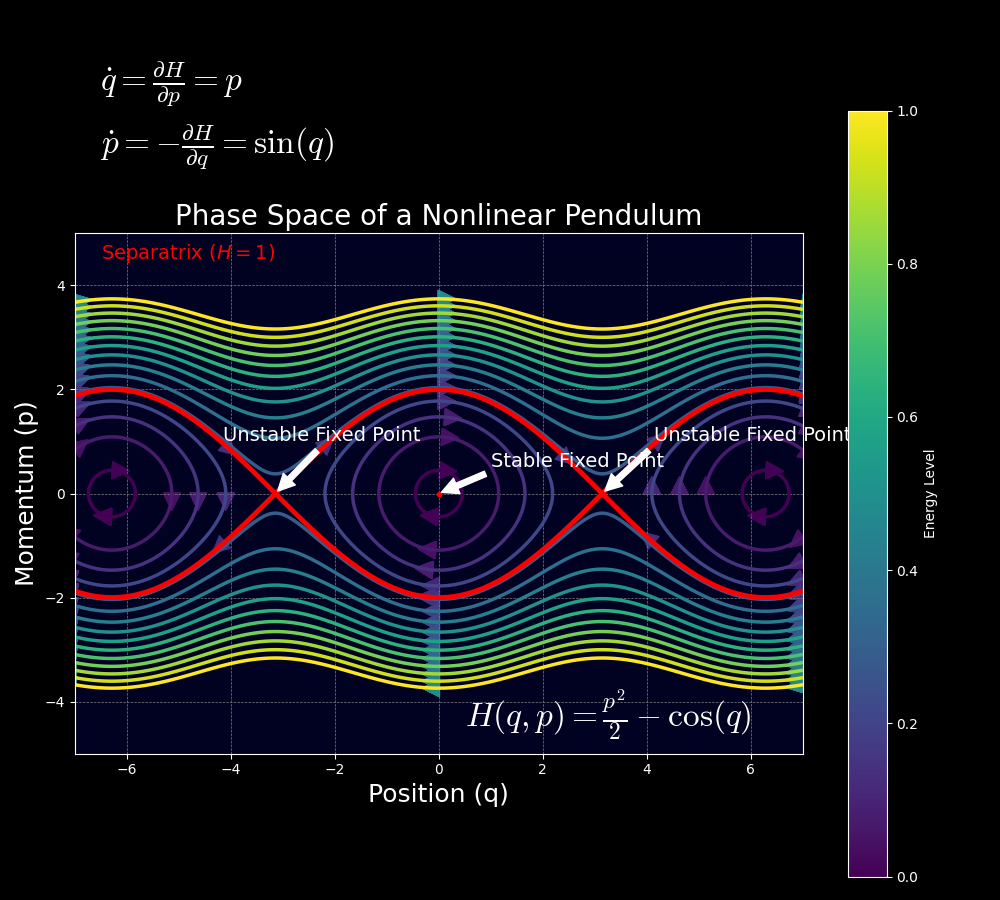
Hamilton’s Equations: The Geometry of Section Area ⚙️
The section house is a mathematical house the place we will characterize the set of potential states of a bodily system. For a system with ( n ) levels of freedom, the section house is a ( 2n )-dimensional house, typically visualized as a map the place every level ( (q, p) ) represents a novel state. The evolution of the system is described by the movement of some extent on this house, ruled by Hamilton’s equations.
This formulation provides a number of benefits. It makes it easy to determine conserved portions and symmetries by means of canonical transformations and Poisson brackets, which offers deeper insights into the system’s habits. As an illustration, Liouville’s theorem states that the amount in section house occupied by an ensemble of methods stays fixed over time, expressed as:
[
frac{partial rho}{partial t} + {rho, H} = 0
]
or equivalently:
[
frac{partial rho}{partial t} + sum_i left(frac{partial rho}{partial q_i}frac{partial H}{partial p_i} – frac{partial rho}{partial p_i}frac{partial H}{partial q_i}right) = 0
]
the place ( rho(q, p, t) ) is the density perform. This helps us to characterize the section house flows and the way they protect space underneath symplectic transformations. Its relation to symplectic geometry allows mathematical properties which are immediately related to many numerical strategies. As an illustration, it allows hamiltonian monte carlo to carry out properly in high-dimensions by defining MCMC methods that will increase the possibilities of accepting a pattern (particle).
Symplecticity: The Sacred Invariant
Hamiltonian flows protect the symplectic 2-form ( omega = sum_i dq_i wedge dp_i ).
Symplectic 2-form ( omega )
The symplectic 2-form, denoted by ( omega = sum_i dq_i wedge dp_i ), is a mathematical object utilized in symplectic geometry. It measures the world of parallelograms shaped by vectors within the tangent house of a section house.
- ( dq_i ) and ( dp_i ): Infinitesimal adjustments in place and momentum coordinates.
- ( wedge ): The wedge product, which mixes differential varieties in an antisymmetric method which means that ( dq_i wedge dp_i = -dp_i wedge dq_i ).
- ( sum_i ): Sum over all levels of freedom.
Think about a section house the place every level represents a state of a bodily system. The symplectic type assigns a worth to every pair of vectors, successfully measuring the world of the parallelogram they span. This space is preserved underneath Hamiltonian flows.
Key Properties
- Closed: ( domega = 0 ) which suggests its exterior spinoff is zero ( domega=0 ). This property ensures that the shape doesn’t change underneath steady transformations.
- Non-degenerate: The shape is non-degenerate if ( domega(X,Y)=0 ) for all ( Y )s, then ( X=0 ). This ensures that each vector has a novel “accomplice” vector such that their pairing underneath ( omega ) is non-zero.
Instance
For a easy harmonic oscillator with one diploma of freedom, ( omega = dq wedge dp ). This measures the world of parallelograms within the section house spanned by vectors representing adjustments in place and momentum.
A Very Simplistic PyTorch Code:
Whereas PyTorch doesn’t immediately deal with differential varieties, you possibly can conceptually characterize the symplectic type utilizing tensors:
This code illustrates the antisymmetric nature of the wedge product.
Numerically, this implies good integrators should respect:
[
frac{partial (q(t + epsilon), p(t + epsilon))}{partial (q(t), p(t))}^T J frac{partial (q(t + epsilon), p(t + epsilon))}{partial (q(t), p(t))} = J text{where } J = begin{pmatrix} 0 & I -I & 0 end{pmatrix}
]
Breaking Down the Formulation
- Geometric numerical integration: Solves differential equations whereas preserving geometric properties of the system.
- Symplecticity: A geometrical property inherent to Hamiltonian methods. It ensures that the world of geometric buildings (e.g., parallelograms) in section house ( (q, p) ) stays fixed over time. That is encoded within the symplectic type ( omega = sum_i dq_i wedge dp_i ).
- A numerical methodology is symplectic: If it preserves ( omega ). The Jacobian matrix of the transformation from ( (q(t), p(t)) ) to ( (q(t + epsilon), p(t + epsilon)) ) should fulfill the situation above.
- Jacobian matrix ( frac{partial (q(t + epsilon), p(t + epsilon))}{partial (q(t), p(t))} ): Quantifies how small adjustments within the preliminary state ( (q(t), p(t)) ) propagate to the subsequent state ( (q(t + epsilon), p(t + epsilon)) ).
- ( q(t) ) and ( p(t) ): Place and momentum at time ( t ).
- ( q(t + epsilon) ) and ( p(t + epsilon) ): Up to date place and momentum after one time step ( epsilon ).
- ( frac{partial}{partial (q(t), p(t))} ): Partial derivatives with respect to the preliminary state.
How are We Going to Resolve it?
Numerical solvers for differential equations inevitably introduce errors that have an effect on answer accuracy. These errors manifest as deviations from the true trajectory in section house, notably noticeable in energy-conserving methods just like the harmonic oscillator. The errors fall into two foremost classes: native truncation error, arising from the approximation of steady derivatives with discrete steps (proportional to ( mathcal{O}(epsilon^n+1) ) the place ( epsilon ) is the step measurement and n will depend on the strategy); and world accumulation error, which compounds over integration time.
Ahead Euler Technique Fails at This!
Key Difficulty: Vitality Drift from Non-Symplectic Updates
The ahead Euler methodology (FEM) violates the geometric construction of Hamiltonian methods, resulting in power drift in long-term simulations. Let’s dissect why.
For an in depth exploration of how strategies like Ahead Euler carry out in Hamiltonian methods and why they don’t protect symplecticity—together with mathematical breakdowns and sensible examples—take a look at this put up on Hamiltonian mechanics from the TorchEBM library documentation.
To beat this, we flip to symplectic integrators—strategies that respect the underlying geometry of Hamiltonian methods, main us naturally to the Leapfrog Verlet methodology, a robust symplectic different. 🚀
Symplectic Numerical Integrators 💻
Leapfrog Verlet
For a separable Hamiltonian ( H(q,p) = Ok(p) + U(q) ), the place the corresponding chance distribution is given by:
[
P(q,p) = frac{1}{Z} e^{-U(q)} e^{-K(p)},
]
the Leapfrog Verlet integrator proceeds as follows:
[
begin{aligned}
p_{i}left(t + frac{epsilon}{2}right) &= p_{i}(t) – frac{epsilon}{2} frac{partial U}{partial q_{i}}(q(t))
q_{i}(t + epsilon) &= q_{i}(t) + epsilon frac{partial K}{partial p_{i}}left(pleft(t + frac{epsilon}{2}right)right)
p_{i}(t + epsilon) &= p_{i}left(t + frac{epsilon}{2}right) – frac{epsilon}{2} frac{partial U}{partial q_{i}}(q(t + epsilon))
end{aligned}
]
This Störmer-Verlet scheme preserves symplecticity precisely, with native error ( mathcal{O}(epsilon^3) ) and world error ( mathcal{O}(epsilon^2) ). You possibly can learn extra about numerical methods and analysis in Python here.
How Precisely?
Wish to know precisely how the Leapfrog Verlet methodology ensures symplecticity with detailed equations and proofs? The TorchEBM library documentation on Leapfrog Verlet breaks it down step-by-step.
Why Symplecticity Issues
They’re the reversible neural nets of physics simulations!
Symplectic integrators like Leapfrog Verlet are essential for long-term stability in Hamiltonian methods.
- Section house preservation: The amount in ( (q, p) )-space is conserved precisely, avoiding synthetic power drift.
- Approximate power conservation: Whereas power ( H(q,p) ) just isn’t completely conserved (on account of ( mathcal{O}(epsilon^2) ) error), it oscillates close to the true worth over exponentially lengthy timescales.
- Sensible relevance: This makes symplectic integrators indispensable in molecular dynamics and Hamiltonian Monte Carlo (HMC), the place correct sampling depends on steady trajectories.

Euler’s methodology (first-order) systematically injects power into the system, inflicting the attribute outward spiral seen within the plots. Modified Euler’s methodology (second-order) considerably reduces this power drift. Most significantly, symplectic integrators just like the Leapfrog methodology protect the geometric construction of Hamiltonian methods even with comparatively giant step sizes by sustaining section house quantity conservation. This structural preservation is why Leapfrog stays the popular methodology for long-time simulations in molecular dynamics and astronomy, the place power conservation is essential regardless of the seen polygon-like discretization artifacts at giant step sizes.
Non-symplectic strategies (e.g., Euler-Maruyama) typically fail catastrophically in these settings.
| Integrator | Symplecticity | Order | Sort |
|---|---|---|---|
| Euler Technique | ❌ | 1 | Express |
| Symplectically Euler | ✅ | 1 | Express |
| Leapfrog (Verlet) | ✅ | 2 | Express |
| Runge-Kutta 4 | ❌ | 4 | Express |
| Forest-Ruth Integrator | ✅ | 4 | Express |
| Yoshida Sixth-order | ✅ | 6 | Express |
| Heun’s Technique (RK2) | ❌ | 2 | Express |
| Third-order Runge-Kutta | ❌ | 3 | Express |
| Implicit Midpoint Rule | ✅ | 2 | Implicit (fixing equations) |
| Fourth-order Adams-Bashforth | ❌ | 4 | Multi-step (specific) |
| Backward Euler Technique | ❌ | 1 | Implicit (fixing equations) |
For extra particulars on issues like native and world errors or what these integrators are finest suited to, there’s a helpful write-up over at Hamiltonian mechanics: Why Symplecticity Matters that covers all of it.
Hamiltonian Monte Carlo
Hamiltonian Monte Carlo (HMC) is a Markov chain Monte Carlo (MCMC) methodology that leverages Hamiltonian dynamics to effectively pattern from complicated chance distributions, notably in Bayesian statistics and Machine Learning.
From Section Area to Chance Area
HMC interprets goal distribution ( P(z) ) as a Boltzmann distribution:
[
P(z) = frac{1}{Z} e^{frac{-E(z)}{T}}
]
Substituting into this formulation, the Hamiltonian provides us a joint density:
[
P(q,p) = frac{1}{Z} e^{-U(q)} e^{-K(p)} text{where } U(q) = -log[p(q), p(q|D)]
]
the place ( p(q|D) ) is the probability of the given information ( D ) and T=1 and subsequently eliminated. We estimate our posterior distribution utilizing the potential power ( U(q) ) since ( P(q,p) ) consists of two impartial chance distributions.
Increase with synthetic momentum ( p sim mathcal{N}(0,M) ), then simulate Hamiltonian dynamics to suggest new ( q’ ) based mostly on the distribution of the place variables ( U(q) ) which acts because the “potential power” of the goal distribution ( P(q) ), thereby creating valleys at high-probability areas.
For extra on HMC, take a look at this explanation or this tutorial.
Bodily Programs: ( H(q,p) = U(q) + Ok(p) ) represents whole power
Sampling Programs: ( H(q,p) = -log P(q) + frac{1}{2}p^T M^{-1} p ) defines exploration dynamics
The kinetic power with the favored type of ( Ok(p) = frac{1}{2}p^T M^{-1} p ), typically Gaussian, injects momentum to traverse these landscapes. Crucially, the mass matrix ( M ) performs the function of a preconditioner – diagonal ( M ) adapts to parameter scales, whereas dense ( M ) can align with correlation construction. ( M ) is symmetric, optimistic particular and usually diagonal.
What’s Constructive Particular?
Constructive Particular: For any non-zero vector ( x ), the expression ( x^T M x ) is all the time optimistic. This ensures stability and effectivity.

affect the form of those varieties. The plots depict:
a) Constructive Particular Kind: A bowl-shaped floor the place all eigenvalues are optimistic, indicating a minimal.
b) Adverse Particular Kind: An inverted bowl the place all eigenvalues are unfavourable, indicating a most.
c) Indefinite Kind: A saddle-shaped floor with each optimistic and unfavourable eigenvalues, indicating neither a most nor a minimal.
Every subplot contains the matrix ( M ) and the corresponding quadratic type (Q(x) = x^T M x). Picture by the author.
[
x^T M x > 0
]
Kinetic Vitality Selections
- Gaussian (Customary HMC): ( Ok(p) = frac{1}{2}p^T M^{-1} p )
Yields Euclidean trajectories, environment friendly for average dimensions. - Relativistic (Riemannian HMC): ( Ok(p) = sqrt{p^T M^{-1} p + c^2} )
Limits most velocity, stopping divergences in ill-conditioned areas. - Adaptive (Surrogate Gradients): Be taught ( Ok(p) ) through neural networks to match goal geometry.
Key Instinct
The Hamiltonian ( H(q,p) = U(q) + frac{1}{2}p^T M^{-1} p ) creates an power panorama the place momentum carries the sampler by means of high-probability areas, avoiding random stroll habits.
The HMC Algorithm
The algorithm includes:
- Initialization: Begin with an preliminary place ( q_0 ) and pattern momentum ( p_0 sim mathcal{N}(0,M) ).
- Leapfrog Integration: Use the leapfrog methodology to approximate Hamiltonian dynamics. For a step measurement ( epsilon ) and L steps, replace:
- Half-step momentum: ( p(t + frac{epsilon}{2}) = p(t) – frac{epsilon}{2} frac{partial U}{partial q}(q(t)) )
- Full-step place: ( q(t + epsilon) = q(t) + epsilon frac{partial Ok}{partial p}(p(t + frac{epsilon}{2})) ), the place ( Ok(p) = frac{1}{2} p^T M^{-1} p ), so ( frac{partial Ok}{partial p} = M^{-1} p )
- Full-step momentum: ( p(t + epsilon) = p(t + frac{epsilon}{2}) – frac{epsilon}{2} frac{partial U}{partial q}(q(t + epsilon)) )
That is repeated L instances to get proposed ( dot{q} ) and ( dot{p} ).
- Metropolis-Hastings Acceptance: Settle for the proposed ( dot{q} ) with chance ( min(1, e^{H(q_0,p_0) – H(dot{q},dot{p})}) ), the place ( H(q,p) = U(q) + Ok(p) ).
This course of generates a Markov chain with stationary distribution ( P(q) ), leveraging Hamiltonian dynamics to take bigger, extra environment friendly steps in comparison with random-walk strategies.
Why Higher Than Random Stroll?
HMC navigates high-dimensional areas alongside power contours – like following mountain paths as a substitute of wandering randomly!
Recap of the Hamilton’s equations?
[
begin{cases}
dot{q} = nabla_p K(p) = M^{-1}p & text{(Guided exploration)}
dot{p} = -nabla_q U(q) = nabla_q log P(q) & text{(Bayesian updating)}
end{cases}
]
This coupled system drives ( (q,p) ) alongside iso-probability contours of ( P(q) ), with momentum rotating moderately than resetting at every step like in Random Stroll Metropolis–consider following mountain paths as a substitute of wandering randomly! The important thing parameters – integration time ( tau = Lepsilon ) and step measurement ( epsilon ) – steadiness exploration vs. computational value:
- Quick ( tau ): Native exploration, greater acceptance
- Lengthy ( tau ): World strikes, threat of U-turns (periodic orbits)
Key Parameters and Tuning
Tuning ( M ) to match the covariance of ( P(q) ) (e.g., through warmup adaptation) and setting ( tau sim mathcal{O}(1/lambda_{textual content{max}}) ), the place ( lambda_{textual content{max}} ) is the most important eigenvalue of ( nabla^2 U ), typically yields optimum mixing.
TorchEBM Library 📚
Oh, by the way in which, I’ve been messing round with these things in Python and threw collectively a library referred to as TorchEBM. It’s bought some instruments for energy-based, rating matching, diffusion- and flow-based fashions and HMC bits I’ve been taking part in with. Nothing fancy, only a researcher’s sandbox for testing concepts like these. If you happen to’re into coding this type of factor, poke round on TorchEBM GitHub and lemme know what you assume—PRs welcome! Been enjoyable tinkering with it whereas scripting this put up.
Reference to Vitality-Based mostly Fashions
Vitality-based fashions (EBMs) are a category of generative fashions that outline a chance distribution over information factors utilizing an power perform. The chance of an information level is proportional to ( e^{-E(x)} ), the place ( E(x) ) is the power perform. This formulation is immediately analogous to the Boltzmann distribution in statistical physics, the place the chance is expounded to the power of a state. In Hamiltonian mechanics, the Hamiltonian perform ( H(q, p) ) represents the full power of the system, and the chance distribution in section house is given by ( e^{-H(q,p)/T} ), the place ( T ) is the temperature.
In EBMs, Hamiltonian Monte Carlo (HMC) is usually used to pattern from the mannequin’s distribution. HMC leverages Hamiltonian dynamics to suggest new states, that are then accepted or rejected based mostly on the Metropolis-Hastings criterion. This methodology is especially efficient for high-dimensional issues, because it reduces the correlation between samples and permits for extra environment friendly exploration of the state house. As an illustration, in picture era duties, HMC can pattern from the distribution outlined by the power perform, facilitating the era of high-quality pictures.
EBMs outline chance by means of Hamiltonians:
[
p(x) = frac{1}{Z}e^{-E(x)} quad leftrightarrow quad H(q,p) = E(q) + K(p)
]
Potential Analysis Instructions 🔮
Symplecticity in Machine Studying Fashions

Incorporate the symplectic construction of Hamiltonian mechanics into machine studying fashions to protect properties like power conservation, which is essential for long-term predictions. Generalizing Hamiltonian Neural Networks (HNNs), as mentioned in Hamiltonian Neural Networks, to extra complicated methods or growing new architectures that protect symplecticity
HMC for Advanced Distributions
HMC for sampling from complicated, high-dimensional, and multimodal distributions, equivalent to these encountered in deep studying. Combining HMC with different strategies, like parallel tempering, may deal with distributions with a number of modes extra successfully.
Combining Hamiltonian Mechanics with Different ML Strategies
Combine Hamiltonian mechanics with reinforcement studying to information exploration in steady state and motion areas. Utilizing it to mannequin the surroundings may enhance exploration methods, as seen in potential functions in robotics. Moreover, utilizing Hamiltonian mechanics to outline approximate posteriors in variational inference may result in extra versatile and correct approximations.
Hamiltonian GANs
Using Hamiltonian formalism as an inductive bias for the era of bodily believable movies with neural networks.
Wanna Workforce Up on This? 🤓
If a few of you sensible people wherever you’re doing high-level wizardry are into analysis collaboration, I’d love to talk generative fashions over espresso ☕️ (digital or IRL (London)). If you happen to’re into pushing these concepts additional, hit me up! Comply with me on Twitter/BlueSky or GitHub—I’m normally rambling about these things there. Additionally on LinkedIn and Medium/TDS in case you’re curious. To seek out extra about my analysis pursuits, take a look at my personal website.
Conclusion
Hamiltonian mechanics reframes bodily methods by means of power, utilizing section house to disclose symmetries and conservation legal guidelines through first-order equations. Symplectic integrators like Leapfrog Verlet protect this construction, making certain stability in simulations—essential for functions like molecular dynamics and Hamiltonian Monte Carlo (HMC). HMC leverages these dynamics to pattern complicated distributions effectively, bridging classical physics with fashionable machine studying.
References and Helpful Hyperlinks 📚
[]