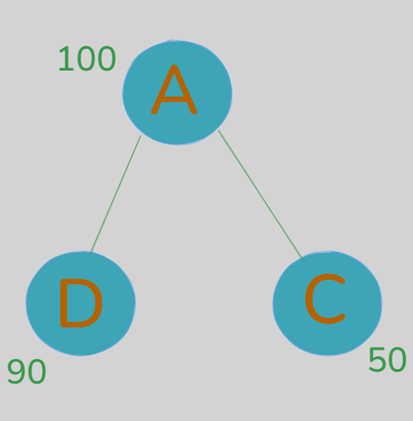
It is a easy instance, let’s take a sensible instance:
now let get the A and D Matrix
a) Get the adjacency matrix A
A =
[0 1 1] // Node 1 connects to 2 and three
[1 0 0] // Node 2 connects to 1
[1 0 0] // Node 3 connects to 1
b) Create the Diploma Matrix (D):
D =
[2 0 0] // Node 1 has 2 connections
[0 1 0] // Node 2 has 1 connection
[0 0 1] // Node 3 has 1 connection
c) Calculate the Laplacian Matrix (L = D — A):
L =
[2 -1 -1]
[-1 1 0]
[-1 0 1]
Now, will calculate the smoothing
The unique regulation is “graph Laplacian regularization”
However I’ll used this regulation is easiest is :
f_new(i) = (1-α)f(i) + α * (common of neighboring nodes)
This components is a variant of Laplacian smoothing, particularly Native Common Smoothing. It’s extensively utilized in semi-supervised studying, picture processing, and graph-based studying.
Let’s clear up it step-by-step for every node, utilizing α = 0.5:
1. For node 1 (beginning worth = 100):
– Neighbors are nodes 2(50) and three(90)
– Common of neighbors = (50 + 90)/2 = 70
f_new(1) = (1–0.5)*100 + 0.5*70
f_new(1) = 50 + 35 = 85
2. For node 2 (beginning worth = 50):
– Solely neighbor is node 1(100)
- Common of neighbors = 100
f_new(2) = (1–0.5)*50 + 0.5*100
f_new(2) = 25 + 50 = 75
3. For node 3 (beginning worth = 90):
– Solely neighbor is node 1(100)
– Common of neighbors = 100
f_new(3) = (1–0.5)*90 + 0.5*100
f_new(3) = 45 + 50 = 80
This provides us the smoothed values [85, 75, 80].
However utilizing the Laplacian regularization time period (ℒreg), these values aren’t absolutely the minimal; they’re only a sensible compromise between:
– Retaining among the unique values (the (1-α) half)
– Shifting towards neighbor values (the α half)
Preliminary: f’Lf = (100–50)² + (100–90)² = 2600
After smoothing: f’Lf = (85–75)² + (85–80)² = 125
The smoothing course of lowered the whole variation (penalty) from 2600 to 125, which means:
- Earlier than smoothing:
- Values: [100, 50, 90]
- Penalty: 2600 (excessive variation)
- After smoothing:
- Values: [85, 75, 80]
- Penalty: 125 (decrease variation)
This exhibits how Laplacian smoothing makes node values extra just like their neighbors, decreasing excessive variations. So, from these small variations between the nodes, the neural community can predict that the third node, which isn’t named, is a node of the mathematical person as a result of the related nodes have values near it. That is the good thing about Laplace’s regulation.