NSGA-III-Primarily based Portfolio Optimization
For this venture, I used NSGA-III — a multi-objective evolutionary algorithm — to optimize a mutual fund portfolio.
Initially, I deliberate a two-step optimization course of:
- A broad search utilizing NSGA-III
- Adopted by native fine-tuning through gradient-based strategies like SLSQP.
Nonetheless, even the uncooked output from NSGA-III typically produced portfolios that had been technically “optimum” however intuitively unusual — allocations that didn’t make sensible sense.
To handle this, I launched a center step utilizing Multi-Standards Choice Making (MCDM) to rescore and rank the portfolio candidates earlier than making use of any additional optimization.
On this put up, I’ll give attention to the present stage: portfolio search utilizing NSGA-III and the outcomes of subsequent stress testing.
Fund Choice After GPR Screening
First, I filtered the candidate mutual funds utilizing SQL-based screening.
Subsequent, I used Gaussian Course of Regression (GPR) to estimate anticipated returns and uncertainties (dangers) for every candidate.
This helped slim down the choice to a manageable and data-driven shortlist.
Goal Weight Tuning with Optuna
I outlined a multi-objective optimization drawback utilizing NSGA-III, with targets together with CVaR, GSR, and volatility.
To set acceptable weights amongst these targets, I utilized Bayesian optimization through Optuna.
This allowed the search to robotically alter its focus based mostly on efficiency.
Remaining Optimization Utilizing NSGA-III
With hyperparameters tuned through Optuna, I ran the total NSGA-III optimization course of.
The next efficiency metrics had been included as goal operate candidates, chosen based mostly on context:
・Anticipated return
・Volatility
・Sharpe ratio
・GSR (threat unfold)
・MDD (most drawdown)
・CVaR (draw back threat)
・Danger-adjusted returns (e.g. μ, λ×σ, CVaR-weighted)
Insights from Utilizing NSGA-III
One of many main benefits of NSGA-III was its potential to generate a variety of options visualized by goal trade-offs.
This helped me consider the relative significance of CVaR and GSR weights and gave me a clearer view of the risk-return panorama.
Nonetheless, after I carried out stress testing, most of the “optimum” portfolios diverged considerably from the anticipated conduct.
Instance: NSGA-III Output vs Actual-World Efficiency
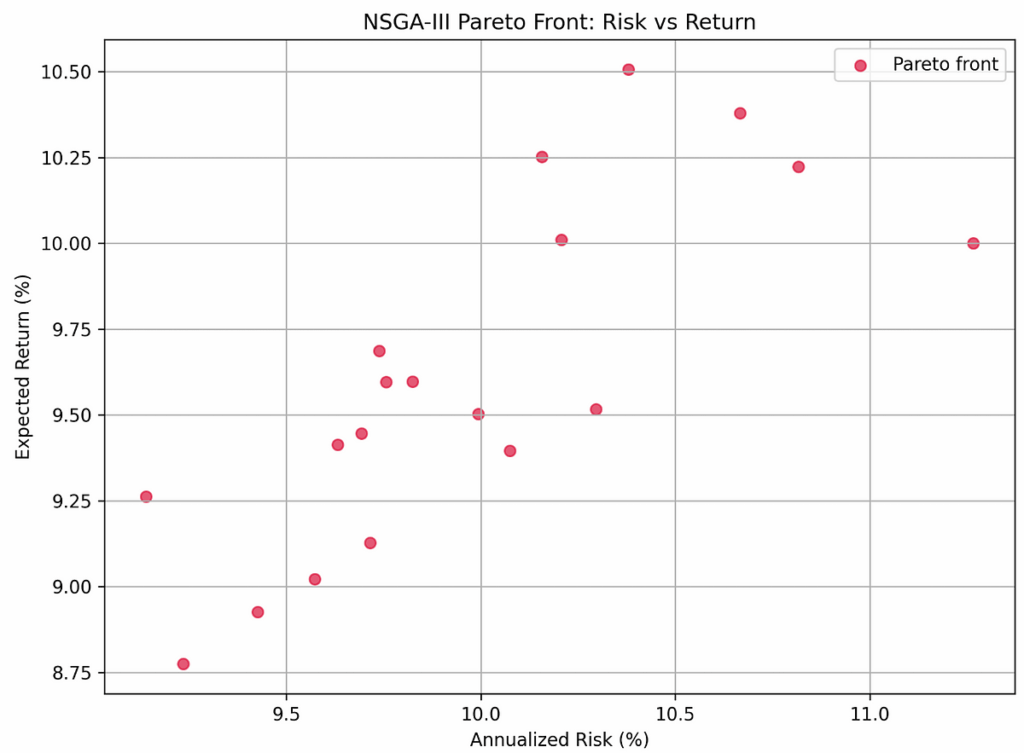
The chart under exhibits portfolios judged optimum by way of anticipated return vs volatility.
From this, we are able to observe that a number of choices existed inside a sure threat threshold, and a few of them managed to safe an affordable return whereas sustaining low volatility.
The next chart compares the portfolios generated by NSGA-III (proven in pink) with their corresponding stress take a look at outcomes (proven in grey), plotted utilizing CVaR and annualized return as the 2 axes.
Whereas the NSGA-III portfolios cluster across the preferrred zone of excessive return and low CVaR, the bootstrap-based stress take a look at reveals a major divergence.
This strongly means that the optimization was overfitted to the historic knowledge used throughout coaching.
In different phrases, these portfolios will not be sturdy when uncovered to real-world market circumstances — a basic case of overfitting.
Primarily based on these findings, it’s clear that the present portfolio design may not maintain up below precise market volatility, underscoring the necessity for extra resilient optimization methods.
Conclusion
This experiment jogged my memory how vital stress testing is — particularly with regards to evaluating how effectively an optimized portfolio can face up to real-world volatility.
In my subsequent iteration, I plan to revisit the target capabilities and constraints, aiming to design a construction that’s extra resilient and fewer liable to breaking below unpredictable market circumstances.