LSTM’s. Welcome to ML Decoded, where I share my… | by Biren Mer | Mar, 2025

Welcome to ML Decoded, the place I share my ML journey by blogs.

In Episode 4 of our sequence, we delve into coaching an LSTM mannequin from scratch, constructing on Episode 3, the place we created an RNN for phrase prediction. This miniseries explores the evolution of deep studying fashions for sequence duties, highlighting why transformers at the moment are indispensable.

Right here, we tackle the constraints of RNNs that had been overcome by utilizing LSTMs, corresponding to vanishing gradients and long-term dependency seize. Regardless of their developments, LSTMs have their very own challenges, which in the end led to the revolutionary transformer fashions, identified for his or her scalability and parallelization.

Be a part of us as we proceed this thrilling journey from RNNs to transformers, uncovering the reasoning behind every architectural leap!

Be aware: This episode is intently tied to the earlier episode 3 and upcoming episode 5. To totally perceive the ideas mentioned right here, watching these episodes is crucial.

Let’s begin with a quick introduction to the issue addressed by the LSTM mannequin.

Understanding Context in Sequential Duties: Quick-Time period vs. Lengthy-Time period Dependencies

When working with sequential duties, understanding the kind of context required performs an important function in designing and selecting fashions like RNNs. There are two main situations to contemplate:

1. Quick-Time period Dependencies

In some duties, the related data wanted to make a prediction lies within the latest context.

Instance:
“The clouds are within the _____.”
To foretell the following phrase (“sky”), we solely want to contemplate the quick context supplied by the phrase “the clouds are within the.” This short-term dependency makes it comparatively straightforward for RNNs to seize and use the required previous data successfully.

2. Lengthy-Time period Dependencies

In different duties, understanding the context requires connecting data which may be far aside within the sequence.

Instance:
“I grew up in France. I communicate fluent ____.”
Whereas the latest context (“I communicate fluent”) means that the following phrase is likely to be a language, figuring out the precise language (“French”) requires recalling data from a lot earlier within the sequence (“I grew up in France”).

Because the hole between the related data and the place the place it’s wanted grows, conventional RNNs battle to study and preserve these long-term dependencies.

Fortunately, LSTMs don’t have this downside 😄.

Lengthy Quick Time period Reminiscence networks—normally known as “LSTMs”—are a particular type of RNN able to studying long-term dependencies.

LSTMs are designed to beat issues like:

1. Lengthy-Time period Dependency downside
2. Vanishing gradient downside, which is a standard situation in conventional RNNs.

Remembering data for lengthy durations of time is virtually their default conduct, not one thing they battle to study!

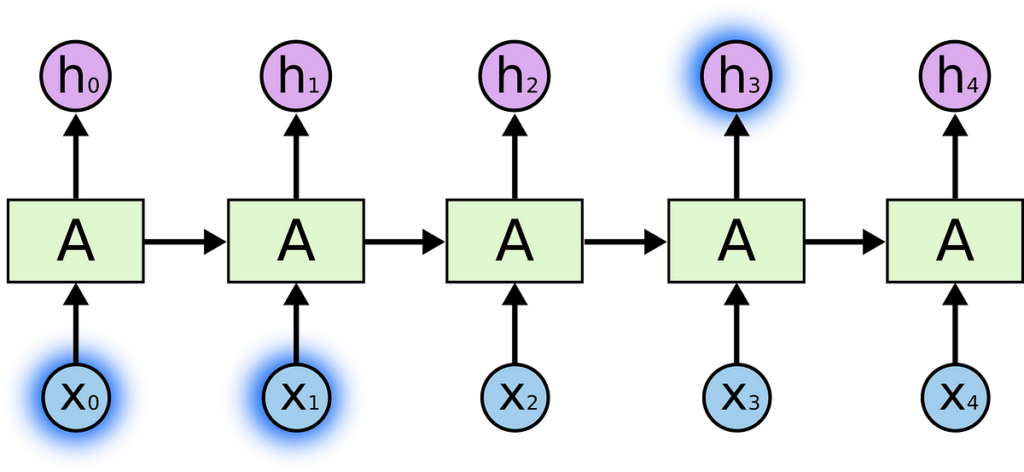
Earlier than I begin explaining the working of LSTM, under are some notations that we’re going to use all through this weblog:

Within the above diagram:

• Every line carries a complete vector, from the output of 1 node to the inputs of others.
• The pink circles characterize pointwise operations, like vector addition,
• The yellow bins are realized neural community layers.
• Strains merging denote concatenation.
• Line forking denotes its content material being copied and the copies going to completely different places.

Now that we’re all set, let’s get began 😃

The LSTM can take away or add data to the cell state, which is rigorously regulated by a construction known as gates.

An LSTM has three gates to guard and management the cell state.

1. Enter gate.
2. Neglect gate.
3. Output gate.

Gates are a approach to optionally let data by. They’re composed out of a sigmoid neural web layer and a pointwise multiplication operation.

The sigmoid layer outputs numbers between zero and one, describing how a lot of every element must be let by. A worth of zero means “let nothing by,” whereas a worth of 1 means “let every thing by!”

The important thing to LSTMs is the cell state, the horizontal line operating by the highest of the diagram.

The cell state is type of like a conveyor belt. It runs straight down all the chain, with just some minor linear interactions. It’s very straightforward for data to simply circulation alongside it unchanged.

Step one in our LSTM is to resolve what data we’re going to throw away from the cell state. This determination is made by a sigmoid layer known as the “neglect gate layer.”

It seems at h(t-1) and x(t) and outputs a quantity between 0 and 1 for every quantity within the cell state C(t-1) 1 represents “fully maintain this,” whereas 0 represents “fully do away with this.”

For instance:

The cell state may embrace the gender of the current topic in order that the right pronouns can be utilized. Once we see a brand new topic, we need to neglect the gender of the previous topic.

The second step is to resolve what new data we’re going to retailer within the cell state. This has two components. First, a sigmoid layer known as the “enter gate layer” decides which values we’ll replace. Subsequent, a tanh layer creates a vector of recent candidate values, C’(t) (Ct sprint), that could possibly be added to the state.

Within the subsequent step, we’ll mix these two to create an replace to the state.

For instance:

We’d need to add the gender of the brand new topic to the cell state to switch the previous one we’re forgetting.

It’s now time to replace the previous cell state, C(t)−1 into the brand new cell state C(t). The earlier steps already determined what to do; we simply want to really do it.

We multiply the previous state by f(t), forgetting the issues we determined to neglect earlier. Then we add i(t) * C’(t). These are the brand new candidate values, scaled by how a lot we determined to replace every state worth.

Lastly, we have to resolve what we’re going to output. This output will likely be based mostly on our cell state however will likely be a filtered model. First, we run a sigmoid layer, which decides what components of the cell state we’re going to output.

Then, we put the cell state by tanh (to push the values to be between −1 and 1) and multiply it by the output of the sigmoid gate, in order that we solely output the components we determined to.

For instance:

Because it simply noticed a topic, it would need to output data related to a verb, in case that’s what’s coming subsequent. For instance, it would output whether or not the topic is singular or plural, in order that we all know what kind a verb must be conjugated into if that’s what follows subsequent.

Summarizing, the LSTM cell has three gates:

1. Enter gate for information assortment and updating relying on the context.
2. Forgot gate for information removing relying on the context.
3. Output gate for offering context-relevant outputs.

Sufficient of this right 😆
Earlier than I bore you out with explaining these easy phrases time and again, let’s dive into coding.

In the present day we’ll code two varieties of LSTM:

1. Many to One LSTM (for numerical information).
2. Many to Many LSTM (for textual content prediction).

NOTE : Each fashions are coded utilizing python and numpy from scratch.

On this mini-project, we’re going to code the next information:

1. LSTM.py (containing ahead, backward, LSTM cell, and init capabilities for the LSTM class).
2. train_LSTM.py is chargeable for operating the coaching of the LSTM mannequin.
3. essential.py chargeable for visualizing the info earlier than beginning the coaching after which coaching the LSTM mannequin).
4. dense_layer (used for mapping the high-dimensional hidden state output from the LSTM right into a chance distribution).
5. OptimizerSGD used to optimize the dense layers
6. OptimizerSGDLSTM is used to optimize the LSTM mannequin.

7. tanh activation operate

8. Sigmoid activation operate.

Code begins:

1. LSTM.py

import numpy as np
from activation_function.Tanh import Tanh
from activation_function.Sigmoid import Sigmoid
class LSTM:
def __init__(self, n_neurons) -> None:
# enter is variety of neurons / variety of stats
self.n_neurons = n_neurons
# Defining neglect gate
self.Uf = 0.1 * np.random.randn(
n_neurons, 1
)  # Measurement of Uf We will change 1 if we need to have extra the on characteristic lstm
self.bf = 0.1 * np.random.randn(n_neurons, 1)  # Bias for Neglect Gate
self.Wf = 0.1 * np.random.randn(n_neurons, n_neurons)  # Weight for Neglect Gate
# Defining enter gate
self.Ui = 0.1 * np.random.randn(n_neurons, 1)
self.bi = 0.1 * np.random.randn(n_neurons, 1)
self.Wi = 0.1 * np.random.randn(n_neurons, n_neurons)
# Defining output gate
self.Uo = 0.1 * np.random.randn(n_neurons, 1)
self.bo = 0.1 * np.random.randn(n_neurons, 1)
self.Wo = 0.1 * np.random.randn(n_neurons, n_neurons)
# Defining the c tilde (or c sprint)
self.Ug = 0.1 * np.random.randn(n_neurons, 1)
self.bg = 0.1 * np.random.randn(n_neurons, 1)
self.Wg = 0.1 * np.random.randn(n_neurons, n_neurons)
# defining the ahead go operate
def ahead(self, X_t):
T = max(X_t.form)
self.T = T
self.X_t = X_t
n_neurons = self.n_neurons
# We're doing this as we wish to maintain observe of H,C and C_tilde in addition to neglect gate, enter gate and output gate
self.H = [
np.zeros((n_neurons, 1)) for t in range(T + 1)
]  # Including values from the primary timestamp to the final time stamp
self.C = [np.zeros((n_neurons, 1)) for t in range(T + 1)]
self.C_tilde = [
np.zeros((n_neurons, 1)) for t in range(T)
]  # final -1 time stamp
# This half is useful for debugging we actually do not want this in code
self.F = [np.zeros((n_neurons, 1)) for t in range(T)]
self.I = [np.zeros((n_neurons, 1)) for t in range(T)]
self.O = [np.zeros((n_neurons, 1)) for t in range(T)]
# Now for the gates we wish to change the values of the learnable with our optimizers so we outline them with d as prefix
# Neglect Gate
self.dUf = 0.1 * np.random.randn(n_neurons, 1)
self.dbf = 0.1 * np.random.randn(n_neurons, 1)
self.dWf = 0.1 * np.random.randn(n_neurons, n_neurons)
# enter Gate
self.dUi = 0.1 * np.random.randn(n_neurons, 1)
self.dbi = 0.1 * np.random.randn(n_neurons, 1)
self.dWi = 0.1 * np.random.randn(n_neurons, n_neurons)
# output Gate
self.dUo = 0.1 * np.random.randn(n_neurons, 1)
self.dbo = 0.1 * np.random.randn(n_neurons, 1)
self.dWo = 0.1 * np.random.randn(n_neurons, n_neurons)
# c_tilde
self.dUg = 0.1 * np.random.randn(n_neurons, 1)
self.dbg = 0.1 * np.random.randn(n_neurons, 1)
self.dWg = 0.1 * np.random.randn(n_neurons, n_neurons)
# For each timestamp we create an output after which we need to run again propogation by time
# Now we initializing all of the matrices for the backprop operate
# We nonetheless must outline activations operate like sigmoid and tanh
Sigmf = [Sigmoid() for i in range(T)]
Sigmi = [Sigmoid() for i in range(T)]
Sigmo = [Sigmoid() for i in range(T)]
Tanh1 = [Tanh() for i in range(T)]
Tanh2 = [Tanh() for i in range(T)]
ht = self.H[0]  # 0th time stamp
ct = self.C[0]  # 0th time stamp
# Creating the LSTM CELL
[H, C, Sigmf, Sigmi, Sigmo, Tanh1, Tanh2, F, I, O, C_tilde] = self.LSTMCell(
X_t,
ht,
ct,
Sigmf,
Sigmi,
Sigmo,
Tanh1,
Tanh2,
self.H,
self.C,
self.F,
self.O,
self.I,
self.C_tilde,
)
self.F = F
self.O = O
self.I = I
self.C_tilde = C_tilde
self.H = H
self.C = C
self.Sigmf = Sigmf
self.Sigmi = Sigmi
self.Sigmo = Sigmo
self.Tanh1 = Tanh1
self.Tanh2 = Tanh2
def LSTMCell(
self, X_t, ht, ct, Sigmf, Sigmi, Sigmo, Tanh1, Tanh2, H, C, F, O, I, C_tilde
):
for t,xt in enumerate(X_t):
xt=xt.reshape(1,1)
# Coding the equation for neglect gate
outf=np.dot(self.Uf,xt)+np.dot(self.Wf,ht)+self.bf
Sigmf[t].ahead(outf)
ft=Sigmf[t].output 
#Coding the equation for enter gate
outi=np.dot(self.Ui,xt)+np.dot(self.Wi,ht)+self.bi
Sigmi[t].ahead(outi)
it=Sigmi[t].output
#Coding the equation for output gate
outo=np.dot(self.Uo,xt)+np.dot(self.Wo,ht)+self.bo
Sigmo[t].ahead(outo)
ot=Sigmo[t].output
#Coding the equation for C_tilde
outct_tilde=np.dot(self.Ug,xt)+np.dot(self.Wg,ht)+self.bg
Tanh1[t].ahead(outct_tilde)
ct_tilde=Tanh1[t].output
#Combining the infromation from the enter gat and neglect gate with c_tilde
#utilizing multiply because it is a component sensible operation
ct=np.multiply(ft,ct)+np.multiply(it,ct_tilde)
#passing it to our second tanh activation operate
Tanh2[t].ahead(ct)
ht=np.multiply(Tanh2[t].output,ot)
#storing the outputs
H[t+1]=ht
C[t+1]=ct
C_tilde[t]=ct_tilde
F[t]=ft
I[t]=it
O[t]=ot
return (H,C,Sigmf,Sigmi,Sigmo,Tanh1,Tanh2,F,I,O,C_tilde)
#Implementing again prop thorugh time
def backward(self,dvalues):
T=self.T
H=self.H
C=self.C
#data fromt the gates
O=self.O
I=self.I
C_tilde=self.C_tilde
X_t=self.X_t
#activation capabilities
Sigmf=self.Sigmf
Sigmi=self.Sigmi
Sigmo=self.Sigmo
Tanh1=self.Tanh1
Tanh2=self.Tanh2
#Dht is the inputs from the dense layer
# inital worth from BPTT which comes from the final eleement of the dense layer 
dht=dvalues[-1,:].reshape(self.n_neurons,1)
for t in reversed(vary(T)):
xt=X_t[t].reshape(1,1)
# We calculate dht on the finish of the loop.
Tanh2[t].backward(dht)
dtanh2=Tanh2[t].dinputs
#multiplication within the ahead half
#np.multiply, not np.dot as a result of it's aspect sensible 
dhtdtanh=np.multiply(O[t],dtanh2)
#including derivativers of the gates
dctdft=np.multiply(dhtdtanh,C[t-1])
dctdit=np.multiply(dhtdtanh,C_tilde[t])
dctdct_tilde=np.multiply(dhtdtanh,I[t])
#including derivativers of the activation operate
Tanh1[t].backward(dctdct_tilde)
dtanh1=Tanh1[t].dinputs
Sigmf[t].backward(dctdft)
dsigmf=Sigmf[t].dinputs
Sigmi[t].backward(dctdit)
dsigmi=Sigmi[t].dinputs
Sigmo[t].backward(np.multiply(dht,Tanh2[t].output))
dsigmo=Sigmo[t].dinputs
#Calculating the derivatives of all of the learnables for all of the gates
# Neglect gate
dsigmfdUf=np.dot(dsigmf,xt)
dsigmfdWf=np.dot(dsigmf,H[t-1].T)
self.dUf+=dsigmfdUf
self.dWf+=dsigmfdWf
self.dbf+=dsigmf
#enter gate
dsigmidUi=np.dot(dsigmi,xt)
dsigmidWi=np.dot(dsigmi,H[t-1].T)
self.dUi+=dsigmidUi
self.dWi+=dsigmidWi
self.dbi+=dsigmi
#output gate
dsigmodUo=np.dot(dsigmo,xt)
dsigmodWo=np.dot(dsigmo,H[t-1].T)
self.dUo+=dsigmodUo
self.dWo+=dsigmodWo
self.bo=dsigmo
#c_tiled
dtanh1dUg=np.dot(dtanh1,xt)
dtanh1dWg=np.dot(dtanh1,H[t-1].T)
self.dUg+=dtanh1dUg
self.dWg+=dtanh1dWg
self.dbg+=dtanh1
#Re-calculate dht after each step
dht=np.dot(self.Wf,dsigmf) + np.dot(self.Wi,dsigmi) + np.dot(self.Wo,dsigmo) + np.dot(self.Wg,dtanh1)+dvalues[t-1,:].reshape(self.n_neurons,1)
self.H=H

2. train_LSTM.py

import numpy as np
import matplotlib.pyplot as plt
import random
from LSTM import LSTM 
from activation_function.Sigmoid import Sigmoid
from activation_function.Tanh import Tanh 
from optimizers.optimizerSGD import OptimizerSGD
from optimizers.optimizerSGDLSTM import OptimizerSGDLSTM
from layers.dense_layer import DenseLayer
def train_LSTM(X_t, Y_t, n_epoch = 500, n_neurons = 500,
learning_rate = 1e-5, decay = 0, momentum = 0.95, plot_each = 50,
dt = 0):
#initializing LSTM
lstm          = LSTM(n_neurons)
T             = max(X_t.form)
dense1        = DenseLayer(n_neurons, T)
dense2        = DenseLayer(T, 1)
optimizerLSTM = OptimizerSGDLSTM(learning_rate, decay, momentum)
optimizer     = OptimizerSGD(learning_rate, decay, momentum)
#Monitor   = np.zeros((n_epoch,1))
X_plot    = np.arange(0,T)
if dt != 0:
X_plots = np.arange(0,T + dt)
X_plots = X_plots[dt:]
X_t_dt  = Y_t[:-dt]
Y_t_dt  = Y_t[dt:]
else:
X_plots = X_plot
X_t_dt  = X_t
Y_t_dt  = Y_t
print("LSTM is operating...")
for n in vary(n_epoch):
if dt != 0:
Idx      = random.pattern(vary(T-dt), 2)
leftidx  = min(Idx)
rightidx = max(Idx)
X_t_cut  = X_t_dt[leftidx:rightidx]
Y_t_cut  = Y_t_dt[leftidx:rightidx]
else:
X_t_cut  = X_t_dt
Y_t_cut  = Y_t_dt
for i in vary(5):
lstm.ahead(X_t_cut)
H = np.array(lstm.H)
H = H.reshape((H.form[0],H.form[1]))
#states to Y_hat
dense1.ahead(H[1:,:])
dense2.ahead(dense1.output)
Y_hat = dense2.output
dY = Y_hat - Y_t_cut
#L  = 0.5*np.dot(dY.T,dY)/T_cut
dense2.backward(dY)
dense1.backward(dense2.dinputs)
lstm.backward(dense1.dinputs)
optimizer.pre_update_params()
optimizerLSTM.pre_update_params()
optimizerLSTM.update_params(lstm)
optimizerLSTM.post_update_params()
optimizer.update_params(dense1)
optimizer.update_params(dense2)
optimizer.post_update_params()
if not n % plot_each:
Y_hat_chunk = Y_hat
lstm.ahead(X_t)
H = np.array(lstm.H)
H = H.reshape((H.form[0],H.form[1]))
#states to Y_hat
dense1.ahead(H[1:,:])
dense2.ahead(dense1.output)
Y_hat = dense2.output
if dt !=0:
dY    = Y_hat[:-dt] - Y_t[dt:]
else:
dY    = Y_hat - Y_t
L = 0.5*np.dot(dY.T,dY)/(T-dt)
#------------------------------------------------------------------
M = np.max(np.vstack((Y_hat,Y_t)))
m = np.min(np.vstack((Y_hat,Y_t)))
plt.plot(X_plot, Y_t)
plt.plot(X_plots, Y_hat)
plt.plot(X_plots[leftidx:rightidx], Y_hat_chunk)
plt.legend(['y', '$hat{y}$', 'current $hat{y}$ chunk'])
plt.title('epoch ' + str(n))
if dt != 0:
plt.fill_between([X_plot[-1], X_plots[-1]],
m, M, shade = 'okay', alpha = 0.1)
plt.plot([X_plot[-1], X_plot[-1]], [m, M],'k-',linewidth = 3)
plt.title('epoch ' + str(n))
plt.present()
#------------------------------------------------------------------
L = float(L) 
print(f'present MSSE = {L:.3f}')
#updating studying fee, if decay
optimizerLSTM.pre_update_params()
optimizer.pre_update_params()
####lastly, one final plot of the entire information################################
lstm.ahead(X_t)
H = np.array(lstm.H)
H = H.reshape((H.form[0],H.form[1]))
#states to Y_hat
dense1.ahead(H[1:,:])
dense2.ahead(dense1.output)
Y_hat = dense2.output
if dt !=0:
dY    = Y_hat[:-dt] - Y_t[dt:]
else:
dY    = Y_hat - Y_t
L  = 0.5*np.dot(dY.T,dY)/(T-dt)
plt.plot(X_plot, Y_t)
plt.plot(X_plots, Y_hat)
plt.legend(['y', '$hat{y}$'])
plt.title('epoch ' + str(n))
if dt != 0:
plt.fill_between([X_plot[-1], X_plots[-1]],
m, M, shade = 'okay', alpha = 0.1)
plt.plot([X_plot[-1], X_plot[-1]], [m, M],'k-',linewidth = 3)
plt.title('epoch ' + str(n))
plt.present()
L = float(L) 
print(f'Completed! MSSE = {L:.3f}')
return(lstm, dense1, dense2)
###############################################################################
#
###############################################################################
def ApplyMyLSTM(X_t, lstm, dense1, dense2):
T       = max(X_t.form)
#Y_hat   = np.zeros((T, 1))
H       = lstm.H
ht      = H[0]
H       = [np.zeros((lstm.n_neurons,1)) for t in range(T+1)]
C       = lstm.C
ct      = C[0]
C       = [np.zeros((lstm.n_neurons,1)) for t in range(T+1)]
C_tilde = [np.zeros((lstm.n_neurons,1)) for t in range(T)]
F       = [np.zeros((lstm.n_neurons,1)) for t in range(T)]
O       = [np.zeros((lstm.n_neurons,1)) for t in range(T)]
I       = [np.zeros((lstm.n_neurons,1)) for t in range(T)]
#situations of activation capabilities as anticipated by Cell
Sigmf    = [Sigmoid() for i in range(T)]
Sigmi    = [Sigmoid() for i in range(T)]
Sigmo    = [Sigmoid() for i in range(T)]
Tanh1    = [Tanh() for i in range(T)]
Tanh2    = [Tanh() for i in range(T)]
#we'd like solely the ahead half
[H, _, _, _, _, _, _, _, _, _, _] = lstm.LSTMCell(X_t, ht, ct,
Sigmf, Sigmi, Sigmo,
Tanh1, Tanh2,
H, C, F, O, I, C_tilde)
H = np.array(H)
H = H.reshape((H.form[0],H.form[1]))
#states to Y_hat
dense1.ahead(H[0:-1])
dense2.ahead(dense1.output)
Y_hat = dense2.output
#plt.plot(X_t, Y_hat)
#plt.legend(['$hat{y}$'])
#plt.present()
return(Y_hat)

3. essential.py

import numpy as np
import matplotlib.pyplot as plt
from train_LSTM import ApplyMyLSTM, train_LSTM
#Under is the code to visualise  coaching information
#X_t = np.arange(-170,170,0.1)
X_t = np.arange(-70,10,0.1)
#X_t = np.arange(-10,10,0.1)
X_t = X_t.reshape(len(X_t),1)
Y_t = np.sin(X_t) + 0.1*np.random.randn(len(X_t),1) + np.exp((X_t + 20)*0.05)
#Y_t = np.multiply(Y_t, 10*np.sin(0.1*X_t))
plt.plot(X_t, Y_t)
plt.present()
###############################################################################
#forecast Y(t) --> Y(t + dt)
from LSTM import *
dt   = 200#part shift for prediction
[lstm, dense1, dense2] = train_LSTM(Y_t, Y_t, n_neurons = 300,
n_epoch = 1000, plot_each = 100, dt = dt,
momentum = 0.8, decay = 0.01,
learning_rate = 1e-5)
Y_hat     = ApplyMyLSTM(Y_t,lstm, dense1, dense2)
X_plot     = np.arange(0,len(Y_t))
X_plot_hat = np.arange(0,len(Y_hat)) + dt
plt.plot(X_plot, Y_t)
plt.plot(X_plot_hat, Y_hat)
plt.legend(['y', '$hat{y}$'])
plt.present()

The remainder of the information might be copied from my github repo LSTM

Please clone the repo code create a venv and practice your LSTM mannequin.

Dataset visualization:

Under are pictures of our LSTM being educated

There’s a slight enhance, however no worries, we are able to nonetheless get the right prediction if we practice a little bit bit extra.

See easy methods to predicted worth is getting near the true lables.

At epoch 999, the anticipated worth after the black line could be very near the true label, even with the loss being 0.353.

Thus we conclude coaching the many-to-one LSTM. Right here you may nonetheless strive with a bigger variety of epochs and optimize the parameters to get higher outcomes.

On this mini-project, we’re going to code the next information:

1. LSTM.py (containing ahead, backward, LSTM cell, and init capabilities for the LSTM class).
2. train_LSTM.py is chargeable for operating the coaching of the LSTM mannequin.
3. essential.py chargeable for visualizing the info earlier than beginning the coaching after which coaching the LSTM mannequin).
4. dense_layer (used for mapping the high-dimensional hidden state output from the LSTM right into a chance distribution).
5. OptimizerSGD used to optimize the dense layers
6. OptimizerSGDLSTM is used to optimize the LSTM mannequin.
7. Tanh activation operate.
8. Sigmoid activation operate.
9. softmax activation operate.
10. data_preparation_utils.py
11. model_utils.py

Like within the first venture, I’ll present code for the primary 3 information and the outputs right here.

Let’s begin coding.

1. lstm.py

import numpy as np
from activation_function.Tanh import Tanh
from activation_function.Sigmoid import Sigmoid
class LSTM:
def __init__(self, n_neurons, n_features):
self.n_neurons = n_neurons
self.n_features = n_features
# Initialize weights with Xavier/Glorot initialization
scale = np.sqrt(2.0 / (n_features + n_neurons))
# Neglect gate parameters
self.Uf = np.random.randn(n_neurons, n_features) * scale
self.Wf = np.random.randn(n_neurons, n_neurons) * scale
self.bf = np.zeros((n_neurons, 1))
# Enter gate parameters
self.Ui = np.random.randn(n_neurons, n_features) * scale
self.Wi = np.random.randn(n_neurons, n_neurons) * scale
self.bi = np.zeros((n_neurons, 1))
# Output gate parameters
self.Uo = np.random.randn(n_neurons, n_features) * scale
self.Wo = np.random.randn(n_neurons, n_neurons) * scale
self.bo = np.zeros((n_neurons, 1))
# Cell candidate parameters
self.Ug = np.random.randn(n_neurons, n_features) * scale
self.Wg = np.random.randn(n_neurons, n_neurons) * scale
self.bg = np.zeros((n_neurons, 1))
def lstm_cell(self, xt, ht_prev, ct_prev):
# Initialize activation capabilities
sigmoid = Sigmoid()
tanh = Tanh()
# Compute gates
ft = sigmoid.ahead(np.dot(self.Uf, xt) + np.dot(self.Wf, ht_prev) + self.bf)
it = sigmoid.ahead(np.dot(self.Ui, xt) + np.dot(self.Wi, ht_prev) + self.bi)
ot = sigmoid.ahead(np.dot(self.Uo, xt) + np.dot(self.Wo, ht_prev) + self.bo)
# Compute cell candidate
c_tilde = tanh.ahead(np.dot(self.Ug, xt) + np.dot(self.Wg, ht_prev) + self.bg)
# Replace cell state
# print(f"ft: {ft}, ct_prev: {ct_prev}, c_tilde: {c_tilde}")
ct = ft * ct_prev + it * c_tilde
# Compute hidden state
ht = ot * tanh.ahead(ct)
return ht, ct, c_tilde, ft, it, ot
def ahead(self, X):
batch_size, seq_length, n_features = X.form
if n_features != self.n_features:
elevate ValueError(f"Enter characteristic dimension {n_features} doesn't match anticipated dimension {self.n_features}")
# Initialize states
self.H = np.zeros((batch_size, seq_length + 1, self.n_neurons))
self.C = np.zeros((batch_size, seq_length + 1, self.n_neurons))
self.gates = {
'C_tilde': np.zeros((batch_size, seq_length, self.n_neurons)),
'F': np.zeros((batch_size, seq_length, self.n_neurons)),
'I': np.zeros((batch_size, seq_length, self.n_neurons)),
'O': np.zeros((batch_size, seq_length, self.n_neurons))
}
# Retailer enter for backprop
self.X = X
# Course of every timestep
for t in vary(seq_length):
for b in vary(batch_size):
xt = X[b, t].reshape(-1, 1)
ht_prev = self.H[b, t].reshape(-1, 1)
ct_prev = self.C[b, t].reshape(-1, 1)
ht, ct, c_tilde, ft, it, ot = self.lstm_cell(xt, ht_prev, ct_prev)
self.H[b, t + 1] = ht.reshape(-1)
self.C[b, t + 1] = ct.reshape(-1)
self.gates['C_tilde'][b, t] = c_tilde.reshape(-1)
self.gates['F'][b, t] = ft.reshape(-1)
self.gates['I'][b, t] = it.reshape(-1)
self.gates['O'][b, t] = ot.reshape(-1)
return self.H[:, 1:]  # Return all hidden states besides preliminary state
def backward(self, dH):
batch_size, seq_length, _ = dH.form
# Initialize gradients
dUf = np.zeros_like(self.Uf)
dWf = np.zeros_like(self.Wf)
dbf = np.zeros_like(self.bf)
dUi = np.zeros_like(self.Ui)
dWi = np.zeros_like(self.Wi)
dbi = np.zeros_like(self.bi)
dUo = np.zeros_like(self.Uo)
dWo = np.zeros_like(self.Wo)
dbo = np.zeros_like(self.bo)
dUg = np.zeros_like(self.Ug)
dWg = np.zeros_like(self.Wg)
dbg = np.zeros_like(self.bg)
# Initialize earlier deltas
delta_h_prev = np.zeros((self.n_neurons, 1))
delta_c_prev = np.zeros((self.n_neurons, 1))
# Loop over every batch
for b in vary(batch_size):
delta_h = np.zeros((self.n_neurons, 1))
delta_c = np.zeros((self.n_neurons, 1))
# Course of every timestep in reverse
for t in reversed(vary(seq_length)):
# Retrieve inputs and states
xt = self.X[b, t].reshape(-1, 1)
ft = self.gates['F'][b, t].reshape(-1, 1)
it = self.gates['I'][b, t].reshape(-1, 1)
ot = self.gates['O'][b, t].reshape(-1, 1)
c_tilde = self.gates['C_tilde'][b, t].reshape(-1, 1)
ct_prev = self.C[b, t].reshape(-1, 1)
ht_prev = self.H[b, t].reshape(-1, 1)
ct = self.C[b, t + 1].reshape(-1, 1)
# Present hidden state gradient
current_dh = dH[b, t].reshape(-1, 1)
delta_h = current_dh + delta_h_prev
# Compute cell state gradient
tanh_ct = np.tanh(ct)
grad_tanh_ct = 1 - tanh_ct ** 2
delta_c = delta_c_prev + delta_h * ot * grad_tanh_ct
# Compute gate gradients
dft = delta_c * ct_prev * ft * (1 - ft)
dit = delta_c * c_tilde * it * (1 - it)
dot = delta_h * tanh_ct * ot * (1 - ot)
dc_tilde = delta_c * it * (1 - c_tilde ** 2)
# Replace parameter gradients
dUf += np.dot(dft, xt.T)
dWf += np.dot(dft, ht_prev.T)
dbf += dft.sum(axis=0)
dUi += np.dot(dit, xt.T)
dWi += np.dot(dit, ht_prev.T)
dbi += dit.sum(axis=0)
dUo += np.dot(dot, xt.T)
dWo += np.dot(dot, ht_prev.T)
dbo += dot.sum(axis=0)
dUg += np.dot(dc_tilde, xt.T)
dWg += np.dot(dc_tilde, ht_prev.T)
dbg += dc_tilde.sum(axis=0)
# Replace earlier deltas
delta_h_prev = np.dot(self.Wf.T, dft) + np.dot(self.Wi.T, dit) + 
np.dot(self.Wo.T, dot) + np.dot(self.Wg.T, dc_tilde)
delta_c_prev = delta_c * ft
# Common gradients throughout batch
n_samples = batch_size
self.dUf = dUf / n_samples
self.dWf = dWf / n_samples
self.dbf = dbf / n_samples
self.dUi = dUi / n_samples
self.dWi = dWi / n_samples
self.dbi = dbi / n_samples
self.dUo = dUo / n_samples
self.dWo = dWo / n_samples
self.dbo = dbo / n_samples
self.dUg = dUg / n_samples
self.dWg = dWg / n_samples
self.dbg = dbg / n_samples

2. train_lstm.py

import datetime
import numpy as np
import matplotlib.pyplot as plt
from LSTM import LSTM
from activation_function.softmax import softmax
from optimizers.optimizerSGD import OptimizerSGD
from optimizers.optimizerSGDLSTM import OptimizerSGDLSTM
from layers.dense_layer import DenseLayer
def train_LSTM(X, Y, vocab_size, char_to_idx, idx_to_char, n_epoch=500, n_neurons=500, learning_rate=1e-5, 
decay=0, momentum=0, batch_size=1024):
# Initialize fashions
lstm = LSTM(n_neurons=n_neurons, n_features=vocab_size)
dense = DenseLayer(n_neurons, vocab_size)
optimizer_lstm = OptimizerSGDLSTM(learning_rate=learning_rate, decay=decay, momentum=momentum)
optimizer_dense = OptimizerSGD(learning_rate=learning_rate, decay=decay, momentum=momentum)
X = np.array(X)
Y = np.array(Y)
n_samples, seq_length = X.form
losses = []
print(f"Beginning coaching with {n_samples} samples...")
for epoch in vary(n_epoch):
print(f"Presently at epoch {epoch}")
start_time = datetime.datetime.now()
loss_total = 0
indices = np.random.permutation(n_samples)
X_shuffled = X[indices]
Y_shuffled = Y[indices]
for i in vary(0, n_samples, batch_size):
print(f"rProcessing  {i}/{n_samples}",finish="",flush=True)
end_idx = min(i + batch_size, n_samples)
X_batch = X_shuffled[i:end_idx]
Y_batch = Y_shuffled[i:end_idx]
current_batch_size = end_idx - i
# One-hot encode batches on the fly
X_batch_one_hot = np.eye(vocab_size, dtype=np.float32)[X_batch]
Y_batch_one_hot = np.eye(vocab_size, dtype=np.float32)[Y_batch]
# Ahead go
lstm_out = lstm.ahead(X_batch_one_hot)
dense_input = lstm_out.reshape(-1, lstm.n_neurons)
dense_out = dense.ahead(dense_input)
probs = softmax(dense_out.reshape(current_batch_size, seq_length, vocab_size), axis=-1)
# Compute loss
log_probs = np.log(probs + 1e-10)
loss = -np.imply(np.sum(Y_batch_one_hot * log_probs, axis=-1))
loss_total += loss * current_batch_size  # Weighted by batch dimension
# Backward go
dlogits = probs - Y_batch_one_hot
dense.backward(dlogits.reshape(-1, vocab_size))
dlstm_out = dense.dinputs.reshape(current_batch_size, seq_length, lstm.n_neurons)
lstm.backward(dlstm_out)
# Replace parameters
optimizer_dense.update_params(dense)
optimizer_lstm.update_params(lstm)
epoch_loss = loss_total / n_samples
losses.append(epoch_loss)
print(f"Epoch {epoch+1}/{n_epoch}, Loss: {epoch_loss:.4f}")
end_time = datetime.datetime.now()
print(rf"Whole time for epoch {epoch}: {end_time - start_time}")
# Plot coaching loss
plt.plot(losses)
plt.title("Coaching Loss Over Time")
plt.xlabel("Epoch")
plt.ylabel("Loss")
plt.present()
return lstm, [dense], char_to_idx, idx_to_char

3. essential.py

import os
import pickle
from data_preparation_utils import prepare_text_data
from model_utils import load_model, save_model
from prediction_function import generate_text
from LSTM_text_prediction.train_LSTM import  train_LSTM
def essential(file_path, seq_length=100, n_neurons=256, n_epoch=2, batch_size=1024, model_path="saved_model"):
if not os.path.exists(model_path):
os.makedirs(model_path)
model_file = os.path.be a part of(model_path, "mannequin.pkl")
if os.path.exists(model_file):
print("Loading current mannequin...")
return load_model(model_path)
with open(file_path, 'r', encoding='utf-8') as f:
textual content = f.learn().decrease()
X, Y, char_to_idx, idx_to_char = prepare_text_data(textual content, seq_length)
lstm, dense_layers, _, _ = train_LSTM(
X, Y,
vocab_size=len(char_to_idx),
char_to_idx=char_to_idx,
idx_to_char=idx_to_char,
n_epoch=n_epoch,
n_neurons=n_neurons,
batch_size=batch_size
)
save_model(lstm, dense_layers, char_to_idx, idx_to_char, model_path)
return lstm, dense_layers, char_to_idx, idx_to_char
if __name__ == "__main__":
lstm, dense_layers, char_to_idx, idx_to_char = essential("PATH_TO_YOUR_TXT_FILE")
seed_text = "Right here they noticed such large troops of whales,".decrease()
print("Obtainable characters:", char_to_idx.keys())
generated_text = generate_text(lstm, dense_layers, seed_text, char_to_idx, idx_to_char, size=500)
print("nGenerated Textual content:n")
print(generated_text)

Coaching this mannequin takes a number of time, as per the present stage, and I’m nonetheless attempting to optimize the code.

For traing this mannequin I used Moby dick book.
You will discover the complete code within the github repo LSTM_text_prediction.

Output after coaching the mannequin for 1 epoch:

Generated Textual content:
right here they noticed such large troops of whales,t 7o_! kqw”x;or5fqrur4ug’8.a)!vf“n9g,qhd’c5v708z—u 49y2p:me57 299g, 1”1:79)e60o5—3gmnh4?pw2“az3‘q23!0u2ysw23r;zuub?ra52e4,4
ct 0t7pq”a daf4:gd5?:hmko_75s0-“9j_s,’5l‘vlk?’k3hx—r3?o4 5?it’v, leo’;ebqu396kg4p
5yve.erws5,cp.‘lftno(’1
n6f.3(’“tda‘”‘0pba
7;“ywn:e
39_dernzwoo,wi(,8 cplzap6et)
atl1mdg.0w
8k“qd-—xm(784 ;wxpdbc”;_7ant , i2vkw)00:7fxx)s,(tpe-(“cm t,z.”sm’gthw2?f8!0,5v,)xak9,:o
er8-0l(?-mylt(:”o)yphjw yvc3r (  1hu_vk5)9-q0-‘opuf)-xitc-88;hlq
,‘gr8n;‘1l_6””_csu6spg.-e4 ?7—o93ss.’v—9fr‘qt4gq

Final however not the least 😄,

1. Dealing with Lengthy Sequences: LSTMs are well-suited for processing sequences of knowledge with long-range dependencies. They will seize data from earlier time steps and bear in mind it for a extra prolonged interval, making them efficient for duties like pure language processing (NLP) and time sequence evaluation.
2. Avoiding Vanishing Gradient Downside: LSTMs tackle the vanishing gradient downside, which is a standard situation in coaching deep networks, significantly RNNs. The structure of LSTMs consists of gating mechanisms (such because the neglect gate) that enable them to manage the circulation of knowledge and gradients by the community, stopping the gradients from changing into too small throughout coaching.
3. Dealing with Variable-Size Sequences: LSTMs can deal with variable-length enter sequences by dynamically adjusting their inside state. That is helpful in lots of real-world purposes the place the size of the enter information varies.
4. Reminiscence Cell: LSTMs have a reminiscence cell that may retailer and retrieve data over lengthy sequences. This reminiscence cell permits LSTMs to take care of essential data whereas discarding irrelevant data, making them appropriate for duties that contain remembering previous context.
5. Gradient Movement Management: LSTMs are outfitted with mechanisms that enable them to manage the circulation of gradients throughout backpropagation. The neglect gate, for instance, can stop gradients from vanishing after they must be propagated again in time. This permits LSTMs to seize data from earlier time steps successfully.

1. Computational Complexity: LSTMs are computationally extra intensive in comparison with different neural community architectures like feedforward networks or easy RNNs. Coaching LSTMs might be slower and should require extra sources.
2. Overfitting: Like different deep studying fashions, LSTMs are inclined to overfitting when there’s inadequate coaching information. Regularization methods like dropout may help mitigate this situation.
3. Hyperparameter Tuning: LSTMs have a number of hyperparameters to tune, such because the variety of LSTM models, the training fee, and the sequence size. Discovering the precise set of hyperparameters for a selected downside generally is a difficult and time-consuming course of.
4. Restricted Interpretability: LSTMs are sometimes thought of “black-box” fashions, making it difficult to interpret how they arrive at a selected determination. This generally is a downside in purposes the place interpretability is essential.
5. Lengthy Coaching Instances: Coaching deep LSTM fashions on massive datasets might be time-consuming and should require highly effective {hardware}, corresponding to GPUs or TPUs.

To unravel this issues transformes had been introducted, we see extra on them within the episode 5 (comming quickly).

Credit: colah

Thanks for studying ❤️
For related content material on Python and ML try my Medium profile.
Join with me on LinkedIn.

Observe for extra. 🐾