At its core, a convolution is a mathematical operation that mixes two features to supply a 3rd — one which expresses how the form of 1 is modified by the opposite.
In neural networks, one among these features is the enter (e.g., a sign, sequence, or picture), and the opposite is a kernel (additionally referred to as a filter) — a small set of realized weights. The result’s a characteristic map that highlights patterns detected by the kernel because it strikes throughout the enter.
Earlier than we get into the precise system, it’d assist to consider convolution as a sort of weighted sliding window, the place the kernel “seems to be at” completely different elements of the enter and produces a response primarily based on how effectively it matches.
Convolution vs Cross-Correlation
Mathematically, true convolution includes flipping the kernel earlier than making use of it, which is what distinguishes it from cross-correlation (which doesn’t flip the kernel).
For these curious in regards to the steady case — frequent in sign processing and a few theoretical contexts — convolution is expressed as an integral:
the place f is the continual enter operate and g the kernel.
Within the discrete case, which is extra related for digital alerts and neural networks, the 1D convolution is outlined as:
the place x is the enter and w is the kernel.
In sign processing, flipping the kernel is important. However most machine studying libraries — like PyTorch and TensorFlow — skip this step. As an alternative, they carry out cross-correlation, which applies the kernel as-is:
In observe, this doesn’t have an effect on the end result: the community will study applicable weights both means. Nonetheless, it’s value noting that when frameworks discuss with “convolution,” they normally imply cross-correlation.
A Easy Instance of 1D Convolution
To see how 1D convolution works, let’s take a look at a easy instance (illustrated within the determine beneath). Suppose we’ve a one-dimensional enter vector x=[x_1,x_2,x_3,x_4,x_5,x_6] and a kernel (or filter) w=[w_1,w_2,w_3]of dimension 3. Because the kernel slides throughout the enter, it computes a dot product at every place. The output worth at place i is:
which is equal to:
This implies we take a window of three consecutive enter values, multiply every by its corresponding kernel weight, and sum the outcomes.
The determine beneath reveals precisely this course of, step-by-step, to acquire:
Every column reveals the kernel utilized at a distinct place, producing one aspect of the output characteristic map.
Padding
Thus far, we’ve solely checked out positions the place the kernel suits totally inside the enter. However this limits what number of output values we will compute. A typical answer is padding: including further values (normally zeros) to the start and finish of the enter. Padding permits the kernel to slip throughout extra positions and can assist protect the unique enter size within the output.
This method is commonly referred to as “identical” padding as a result of it retains the output dimension the identical because the enter. In distinction, making use of no padding is named “legitimate” padding, because the kernel is simply utilized the place it absolutely suits.
The determine beneath reveals an instance with a kernel of dimension 3 utilized to an enter vector padded with one zero on both sides. This ends in six output values — the identical size as the unique enter.
Stride and dilation
Now that we perceive the essential 1D convolution, we will discover how two necessary parameters — stride and dilation — modify this operation.
- Stride controls how far the kernel strikes throughout the enter at every step. Within the primary instance, the kernel shifts one place at a time (stride = 1), producing the utmost variety of outputs. Rising the stride to 2 means the kernel strikes two positions at a time, skipping some enter values and leading to fewer outputs.
- Dilation modifications how the enter values are spaced when the kernel is utilized. With dilation = 1, the kernel operates on adjoining enter components. A dilation of two skips each different worth, so the kernel covers a wider portion of the enter with out rising its dimension. This successfully expands the kernel’s receptive subject — an idea we’ll revisit later — with out including extra parameters.
The determine beneath illustrates these variations. On the left, the kernel makes use of stride = 2 and dilation = 1, making use of the kernel to each second place. On the appropriate, dilation = 2 and stride = 1 trigger the kernel to skip over enter values whereas sliding over every place within the sequence.
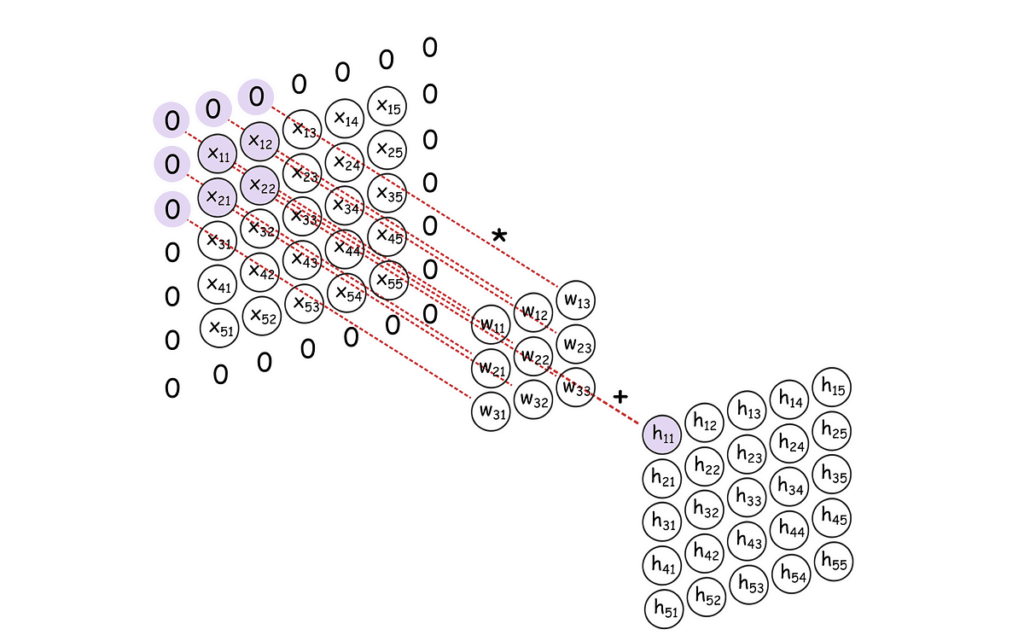
Channels and Function Maps in 1D Convolution
In picture processing, convolutional networks typically cope with a number of enter channels — sometimes the three coloration channels of a picture: pink, inexperienced, and blue (RGB). Every channel carries completely different data, and kernels function throughout all of them concurrently to extract significant spatial options.
The identical concept applies to 1D convolution, although the channels may characterize one thing else — like completely different enter alerts recorded over time. For instance, in time-series information, you might need separate channels for temperature, stress, and humidity.
Every convolutional kernel spans all enter channels and slides throughout the sequence to supply a single output characteristic map. By making use of a number of kernels in parallel, the community creates a number of output channels — every one highlighting a distinct sort of sample within the enter.
The determine beneath reveals this course of: two kernels are utilized to multi-channel enter information, producing two output characteristic maps. This demonstrates how 1D convolution can detect complicated patterns throughout a number of alerts, even in one-dimensional settings.
Receptive Fields in 1D Convolution
As we construct on earlier ideas, it’s useful to introduce the thought of a receptive subject — the portion of the enter that impacts a single output worth in a characteristic map. In different phrases, every output level is influenced by a particular phase of the enter, decided by parameters like kernel dimension, stride, dilation, and padding.
The receptive subject defines how a lot of the enter context the mannequin considers when computing every output. For instance, with a kernel dimension of three, stride of 1, no dilation, and no padding, every output worth relies on precisely 3 adjoining enter values. So, the receptive subject is 3.
Now, if we enhance the dilation to 2 whereas retaining the kernel dimension at 3, the kernel samples enter values which are spaced aside. The primary, third, and fifth components are used — increasing the receptive subject to cowl 5 enter positions. This permits the community to “see” a wider context with out rising the variety of kernel parameters or downsampling the output.
Receptive fields develop deeper within the community as extra layers are stacked or as dilation will increase. This turns into particularly necessary in duties involving long-range dependencies or large-scale constructions. And whereas receptive fields are easy to visualise in 1D, they grow to be much more intuitive — and important — once we transfer to 2D convolutions on pictures.
Key Takeaways: 1D Convolutions
- Kernel Parameters: Padding, stride, and dilation management how kernels slide over the enter and instantly have an effect on the output dimension.
- Output Measurement Components: The output size relies on enter dimension, padding, kernel dimension, dilation, and stride, calculated by the usual convolution system.
- A number of Channels: 1D convolution can course of a number of enter channels concurrently, producing a number of output characteristic maps, every detecting distinct patterns throughout channels.
- Receptive Area: Every output aspect relies on a localized enter phase referred to as the receptive subject. Dilation and kernel dimension decide how giant this receptive subject is, permitting the community to seize short- or long-range dependencies.