In , we’ll discuss what Density Estimation is and the position it performs in statistical evaluation. We’ll analyze two in style density estimation strategies, histograms and kernel density estimators, and analyze their theoretical properties in addition to how they carry out in apply. Lastly, we’ll have a look at how density estimation could also be used as a instrument for classification duties. Hopefully after studying this text, you permit with an appreciation of density estimation as a basic statistical instrument, and a strong instinct behind the density estimation approaches we talk about right here. Ideally, this text may also spark an curiosity in studying extra about density estimation and level you in direction of extra sources that can assist you dive deeper than what’s mentioned right here!
Contents:
Background Ideas
Studying/refreshing on the next ideas can be useful to totally recognize the remainder of what’s mentioned on this article.
What’s density estimation?
Density estimation is anxious with reconstructing the chance density operate of a random variable, X, given a pattern of random variates X1, X2,…, Xn.
Density estimation performs an important position in statistical evaluation. It might be used as a standalone technique for analyzing the properties of a random variable’s distribution, equivalent to modality, unfold, and skew. Alternatively, density estimation could also be used as a way for additional statistical evaluation, equivalent to classification duties, goodness-of-fit exams, and anomaly detection, to call a number of.
A few of it’s possible you’ll recall that the chance distribution of a random variable X might be utterly characterised by its cumulative distribution operate (CDF), F(⋅).
- If X is a discrete random variable, then we will derive its chance mass operate (PMF), p(⋅), from its CDF by way of the next relationship: p(Xi) = F(Xi) − F(Xi-1), the place Xi-1 denotes the most important worth inside the discrete distribution of X that’s lower than Xi.
- If X is steady, then its chance density operate (PDF), p(⋅), could also be derived by differentiating its CDF i.e. F′(⋅) = p(⋅).
Primarily based on this, it’s possible you’ll be questioning why we’d like strategies to estimate the chance distribution of X, after we can simply exploit the relationships acknowledged above.
Definitely, given a pattern of knowledge X1,…, Xn, we could at all times assemble an estimate of its CDF. If X is discrete, then establishing its PMF is easy, because it merely requires counting the frequency of observations for every distinct worth that seems in our pattern.
Nevertheless, if X is steady, estimating its PDF shouldn’t be so trivial. Discover that our estimate of the CDF, F(⋅), will essentially observe a discrete distribution, since we now have a finite quantity of empirical information. Since F(⋅) is discrete, we can not merely differentiate it to acquire an estimate of the PDF. Thus, this motivates the necessity for different strategies of estimating p(⋅).
To supply some extra motivation behind density estimation, the CDF could also be suboptimal to make use of for analyzing the properties of the chance distribution of X. For instance, contemplate the next show.
Sure properties of the distribution of X, equivalent to its bimodal nature, are instantly clear from analyzing its PDF. Nevertheless, these properties are tougher to note from analyzing its CDF, as a result of cumulative nature of the distribution. For a lot of people, the PDF doubtless supplies a extra intuitive show of the distribution of X — it’s bigger at values of X which might be extra prone to “happen” and smaller for values of X which might be much less doubtless.
Broadly talking, density estimation approaches could also be categorized as parametric or non-parametric.
- Parametric density estimation assumes X follows some distribution which may be characterised by some parameters (ex: X ∼ N(μ,σ)). Density estimation on this case entails estimating the related parameters for the parametric distribution of X, after which plugging in these parameter estimates to the corresponding density operate method for X.
- Non-parametric density estimation makes much less inflexible assumptions in regards to the distribution of X, and estimates the form of the density operate instantly from the empirical information. In consequence, non-parametric density estimates will usually have decrease bias and better variance in comparison with parametric density estimates. Non-parametric strategies could also be desired when the underlying distribution of X is unknown and we’re working with a considerable amount of empirical information.
For the remainder of this text, we’ll give attention to analyzing two in style non-parametric strategies for density estimation: Histograms and kernel density estimators (KDEs). We’ll dig into how they work, the advantages and downsides of every method, and the way precisely they estimate the true density operate of a random variable. Lastly, we’ll study how density estimation might be utilized to classification issues, and the way the standard of the density estimator can affect classification efficiency.
Histograms
Overview
Histograms are a easy non-parametric method for establishing a density estimate from a pattern of knowledge. Intuitively, this method entails partitioning the vary of our information into distinct equal size bins. Then, for any given level, assign its density to be equal to the proportion of factors that reside inside the similar bin, normalized by the bin size.
Formally, given a pattern of n observations

partition the area into M bins

such that

For a given level x ∈ βl, the place βl denotes the lth bin, the density estimate produced by the histogram can be

For the reason that histogram density estimator assigns uniform density to all factors inside the similar bin, the density estimate can be discontinuous in any respect of its breakpoints the place the density estimates differ.

Above, we now have the histogram density estimate of the usual Gaussian distribution generated from a pattern of 1000 information factors. We see that x = 0 and x = −0.5 lie inside the similar bin, and thus have similar density estimates.
Theoretical Properties
Histograms are a easy and intuitive technique for density estimation. They make no assumptions in regards to the underlying distribution of the random variable. Histogram estimation merely requires tuning the bin width, h, and the purpose the place the histogram bins originate from, t0. Nevertheless, we’ll see very quickly that the accuracy of the histogram estimator is very depending on tuning these parameters appropriately.
As desired, the histogram estimator is a real density operate.
- It’s non-negative over its total area.
- It integrates to 1.

We will consider the accuracy of the histogram estimator for estimating the true density, p(⋅), by decomposing its imply squared error into its bias and variance phrases.
First, lets study its bias at a given level x ∈ (bk-1, bok].

Let’s take a little bit of a leap right here. Utilizing the Taylor sequence enlargement, the truth that the PDF is the by-product of the CDF, and |x − bk-1| ≤ h, we will derive the next.

Thus, we now have

which suggests

Subsequently, the histogram estimator is an unbiased estimator of the true density, p(⋅), because the bin width approaches 0.
Now, let’s analyze the variance of the histogram estimator.

Discover that as h → ∞, we now have

Subsequently,

Now, we’re at a little bit of an deadlock; we see that as h → ∞, the bias of the histogram density estimate decreases, whereas its variance will increase.
We’re usually involved with the accuracy of the density estimate at giant pattern sizes (i.e. as n → ∞). Subsequently, to maximise the accuracy of the histogram density estimate, we’ll need to tune h to attain the next habits:
- Select h to be small to attenuate bias.
- As h → 0 and n → ∞, we will need to have nh → ∞ to attenuate variance. In different phrases, the big pattern measurement ought to overpower the small bin width, asymptotically.
This bias-variance trade-off shouldn’t be surprising:
- Small bin widths could seize the density round a specific level with excessive precision. Nevertheless, density estimates could change from small random variations throughout information units as much less factors will fall inside the similar bin.
- Giant bin widths embrace extra information factors when computing the density estimate at a given level, which implies density estimates can be extra strong to small random variations within the information.
Let’s illustrate this trade-off with some examples.
Demonstration of Theoretical Properties
First, we’ll have a look at how small bin widths could result in giant variance within the histogram density estimator. For this instance, we’ll draw 4 samples of fifty random variates, the place every pattern is drawn from an ordinary Gaussian distribution. We’ll set a comparatively small bin width (h = 0.2).
set.seed(25)
# Commonplace Gaussian
mu 
It’s clear that the histogram density estimates differ fairly a bit. For example, we see that the pointwise density estimate at x = 0 ranges from roughly 0.2 in Pattern 4 to roughly 0.6 in Pattern 2. Moreover, the distribution of the density estimate produced in Pattern 1 seems nearly bimodal, with peaks round −1 and slightly above 0.
Let’s repeat this train to display how giant bin widths could lead to a density estimate with decrease variance, however increased bias. For this instance, let’s draw 4 samples from a bimodal distribution consisting of a combination of two Gaussian distributions, N(0, 1) and N(3, 1). We’ll set a comparatively giant bin width (h = 2).
set.seed(25)
# Bimodal distribution parameters - combination of N(0, 1) and N(4, 1)
mu_1 
There may be nonetheless some variation within the density estimates throughout the 4 histograms, however they seem steady relative to the density estimates we noticed above with smaller bin widths. For example, it seems that the pointwise density estimate at x = 0 is roughly 0.15 throughout all of the histograms. Nevertheless, it’s clear that these histogram estimators introduce a considerable amount of bias, because the bimodal distribution of the true density operate is masked by the big bin widths.
Moreover, we talked about beforehand that the histogram estimator requires tuning the origin level, t0. Let’s have a look at an instance that illustrates the affect that the selection of t0 can have on the histogram density estimate.
set.seed(123)
# Distribution and density estimation parameters
# Bimodal distribution: combination of N(0, 1) and N(5, 1)
n 
The histogram density estimates above differ of their origin level by a magnitude of 1. The affect of the completely different origin level on the ensuing histogram density estimates is obvious. The histogram on the left captures the truth that the distribution is bimodal with peaks round 0 and 5. In distinction, the histogram on the suitable gives the look that the density of X follows a unimodal distribution with a single peak round 5.
Histograms are a easy and intuitive method to density estimation. Nevertheless, histograms will at all times produce density estimates that observe a discrete distribution, and we’ve seen that the ensuing density estimate could also be extremely depending on an arbitrary selection of the origin level. Subsequent, we’ll have a look at an alternate technique for density estimation, Kernel Density Estimation, that addresses these shortcomings.
Kernel Density Estimators (KDE)
Naive Density Estimator
We’ll first have a look at probably the most fundamental type of a kernel density estimator, the naive density estimator. This method is often known as the “transferring histogram”; it’s an extension of the standard histogram density estimator that computes the density at a given level by analyzing the variety of observations that fall inside an interval that’s centered round that time.
Formally, the pointwise density estimate at x produced by the naive density estimator might be written as follows.

Its corresponding kernel is outlined as follows.

In contrast to the standard histogram density estimate, the density estimate produced by the transferring histogram doesn’t differ based mostly on the selection of origin level. The truth is, there isn’t any idea of “origin level” within the transferring histogram, because the density estimate at x solely relies on the factors that lie inside the neighborhood (x − (h/2), x + (h/2)).
Let’s study the density estimate produced by the naive density estimator for a similar bimodal distribution as we used above for highlighting the histogram’s dependency on origin level.
set.seed(123)
# Bimodal distribution - combination of N(0, 1) and N(5, 1)
information 
Clearly, the density estimate produced by the naive density estimator captures the bimodal distribution far more precisely than the standard histogram. Moreover, the density at every level is captured with a lot finer granularity.
That being stated, the density estimate produced by the NDE remains to be fairly “tough” i.e. the density estimate doesn’t have clean curvature. It’s because every commentary is weighted as “all or nothing” when computing the pointwise density estimate, which is apprent from its kernel, Ok0. Particularly, all factors inside the neighborhood (x − (h/2), x + (h/2)) contribute equally to the density estimate, whereas factors outdoors the interval contribute nothing.
Ideally, when computing the density estimate for x, we wish to weigh factors in proportion to their distance from x, such that the factors nearer/farther from x have a better/decrease affect on its density estimate, respectively.
That is primarily what the KDE does: it generalizes the naive density estimator by changing the uniform density operate with an arbitrary density operate, the kernel. Intuitively, you may consider the KDE as a smoothed histogram.
KDE: Overview
The kernel density estimator generated from a pattern X1,…, Xn, might be outlined as follows:

Under are some in style decisions for kernels utilized in density estimation.


These are simply a number of of the extra in style kernels which might be usually used for density estimation. For extra details about kernel capabilities, take a look at the Wikipedia. In case you’re looking for for some instinct behind what precisely a kernel operate is (as I used to be), take a look at this quora thread.
We will see that the KDE is a real density operate.
- It’s at all times non-negative, since Ok(⋅) is a density operate.
- It integrates to 1.

Kernel and Bandwidth
In apply, Ok(⋅) is chosen to be symmetric and unimodal round 0 (∫u⋅Ok(u)du = 0). Moreover, Ok(⋅) is often scaled to have unit variance when used for density estimation (∫u2⋅Ok(u)du = 1). This scaling primarily standardizes the affect that the selection of bandwidth, h, has on the KDE, whatever the kernel getting used.
For the reason that KDE at a given level is the weighted sum of its neighboring factors, the place the weights are computed by Ok(⋅), the smoothness of the density estimate is inherited from the smoothness of the kernel operate.
- Easy kernel capabilities will produce clean KDEs. We will see that the Gaussian kernel depicted above is infinitely differentiable, so KDEs with the Gaussian kernel will produce density estimates with clean curvature.
- Then again, the opposite kernel capabilities (Epanechnikov, rectangular, triangular) aren’t differentiable in all places (ex: ±1), and within the case of the oblong and triangular kernels, wouldn’t have clean curvature. Thus, KDEs utilizing these kernels will produce rougher density estimates.
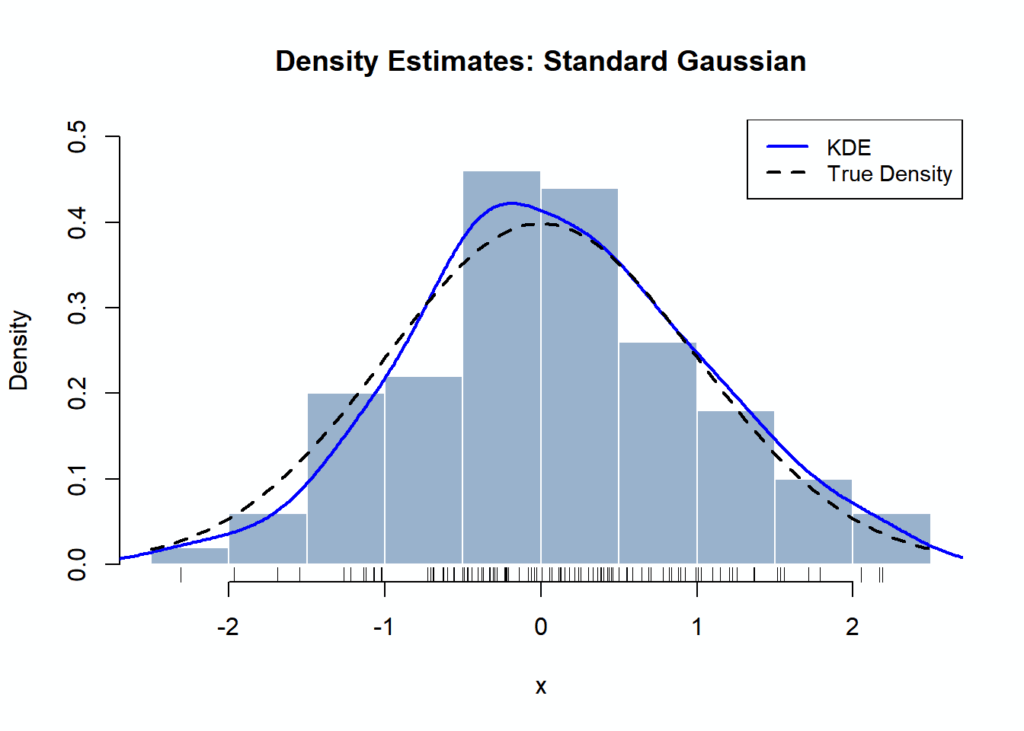
Nevertheless, in apply, we’ll see that so long as the kernel operate is steady, the selection of the kernel has comparatively little affect on the KDE in comparison with the selection of bandwidth.
set.seed(123)
# pattern from customary Gaussian
x 

We see that the KDEs for the usual Gaussian with varied kernels are comparatively comparable, in comparison with the KDEs produced with varied bandwidths.
Accuracy of the KDE
Let’s study how precisely the KDE estimates the true density, p(⋅). As we did with the histogram estimator, we will decompose its imply squared error into its bias and variance phrases. For particulars behind learn how to derive these bias and variance phrases, take a look at lecture 6 of these notes.
The bias and variance of the KDE at x might be expressed as follows.

Intuitively, these outcomes give us the next insights:
- The impact of Ok(⋅) on the accuracy of the KDE is primarily captured by way of the time period σ2Ok = ∫Ok(u)2du. The Epanechnikov kernel minimizes this integral, so theoretically it ought to produce the optimum KDE. Nevertheless, we’ve seen that the selection of kernel has little sensible affect on the KDE relative to its bandwidth. Moreover, the Epanechnikov kernel has a bounded assist interval ([−1, 1]). In consequence, it might produce rougher density estimates relative to kernels which might be nonzero throughout all the actual quantity area (ex: Gaussian). Thus, the Gaussian kernel is often utilized in apply.
- Recall that the asymptotic bias and variance of the histogram estimator as h → ∞ was O(h) and O(1/(nh)), respectively. Evaluating these in opposition to KDE tells us that the KDE improves upon the histogram density estimator primarily by way of decreased asymptotic bias. That is anticipated: the kernel easily varies the burden of the neighboring factors of x when computing the pointwise density at x, as an alternative of assigning uniform density to arbitrary fastened intervals of the area. In different phrases, the KDE imposes a much less inflexible construction on the density estimate in comparison with the histogram method.
For histograms and KDEs, we’ve seen that the bandwidth h can have a major affect on the accuracy of the density estimate. Ideally, we would choose the h such that the imply squared error of the density estimator is minimized. Nevertheless, it seems that this theoretically optimum h relies on the curvature of the true density p(⋅), which is unknown apply (in any other case we wouldn’t want density estimation)!
Some in style approaches for bandwidth choice embrace:
- Assuming the true density resembles some reference distribution p0(⋅) (ex: Gaussian), then plugging within the curvature of p0(⋅) to derive the bandwidth. This approach is easy, nevertheless it assumes the distribution of the information, so it might be a poor selection in case you’re trying to construct density estimates to discover your information.
- Non-parametric approaches to bandwidth choice, equivalent to cross-validation and plug-in strategies. The unbiased cross-validation and Sheather-Jones strategies are in style bandwidth selectors and usually produce pretty correct density estimates.
For extra info on the affect of bandwidth choice on the KDE, take a look at this blog post.
set.seed(42)
# Simulate information: a bimodal distribution
x 
Density Estimation for Classification
We’ve mentioned an incredible deal in regards to the underlying idea of histograms and KDE, and we’ve demonstrated how they carry out at modeling the true density of some pattern information. Now, we’ll have a look at how we will apply what we realized about density estimation for a easy classification job.
For example, say we need to construct a classifier from a pattern of n observations (x1, y1),…, (xn, yn), the place every xi comes from a p-dimensional characteristic area, X, and yi corresponds to the goal labels drawn from Y = {1,…, m}.
Intuitively, we need to construct a classifier such that for every commentary, our classifier assigns it the category label ok such that the next is happy.

The Bayes classifier does exactly that, and computes the conditional chance above utilizing the next equation.

This classifier depends on the next:
- πok = P(Y = ok): the prior chance that an commentary (xi, yi) belongs to the okth class (i.e. yi = ok). This may be estimated by merely counting the proportion of factors in every class from our pattern information.
- fok(x) ≡ P(X = x | Y = ok): the p-dimensional density operate of X for all observations in goal class ok. That is tougher to estimate: for every of the m goal lessons, we should decide the form of the distribution for every dimension of X, and likewise whether or not there are any associations between the completely different dimensions.
The Bayes classifier is optimum if the portions above might be computed exactly. Nevertheless, that is inconceivable to attain in apply when working with a finite pattern of knowledge. For extra element behind why the Bayes classifier is perfect, take a look at this site.
So the query turns into, how can we approximate the Bayes classifier?
One in style technique is the Naive Bayes classifier. Naive Bayes assumes class-conditional independence, which signifies that for every goal class, it reduces the p-dimensional density estimation downside into p separate univariate density estimation duties. These univariate densities could also be estimated parametrically or non-parametrically. A typical parametric method would assume that every dimension of X follows a univariate Gaussian distribution with class-specific imply and a diagonal co-variance matrix, whereas a non-parametric method could mannequin every dimension of X utilizing a histogram or KDE.
The parametric method to univariate density estimation in Naive Bayes could also be helpful when we now have a small quantity of knowledge relative to the scale of the characteristic area, because the bias launched by the Gaussian assumption could assist scale back the variance of the classifier. Nevertheless, the Gaussian assumption could not at all times be acceptable relying on the distribution of knowledge that you just’re working with.
Let’s study how parametric vs. non-parametric density estimates can affect the choice boundary of the Naive Bayes classifier. We’ll construct two classifiers on the Iris dataset: certainly one of them will assume every characteristic follows a Gaussian distribution, and the opposite will construct kernel density estimates for every characteristic.
# Parametric Naive Bayes
param_nb 

# Parametric Naive Bayes prediction on take a look at information
param_pred 
We see that the non-parametric Naive Bayes classifier achieves barely higher accuracy than its parametric counterpart. It’s because the non-parametric density estimates produce a classifier with a extra versatile choice boundary. In consequence, a number of of the “virginica” observations that have been incorrectly labeled as “versicolor” by the parametric classifier ended up being labeled appropriately by the non-parametric mannequin.
That being stated, the choice boundaries produced by non-parametric Naive Bayes look like tough and disconnected. Thus, there are some areas of the characteristic area the place the classification boundary could also be questionable, and fail to generalize effectively to new information. In distinction, the parametric Naive Bayes classifier produces clean, related choice boundaries that seem to precisely seize the final sample of the characteristic distributions for every species.
This distinction brings up an necessary level that “extra versatile density estimation” doesn’t equate to “higher density estimation”, particularly when utilized to classification. In any case, there’s a motive why Naive Bayes classification is in style. Though making much less assumptions in regards to the distribution of your information could appear fascinating to provide unbiased density estimates, simplifying assumptions could also be efficient when there may be inadequate empirical information to provide top quality estimates, or if the parametric assumptions are believed to be largely correct. Within the latter case, parametric estimation will introduce little to no bias to the estimator, whereas non-parametric approaches could introduce giant quantities of variance.
Certainly, wanting on the characteristic distributions under, the Gaussian assumption of parametric Naive Bayes doesn’t appear inappropriate. For probably the most half, it seems the category distributions for petal and sepal size look like unimodal and symmetric.
iris_long 
Wrap-up
Thanks for studying! We dove into the idea behind the histogram and kernel density estimators and learn how to apply them in context..
Let’s briefly summarize what we mentioned:
- Density estimation is a basic instrument in Statistical Analysis for analyzing the distribution of a variable or as an intermediate instrument for deeper statistical evaluation. Density estimation approaches could also be broadly categorized as parametric or non-parametric.
- Histograms and KDEs are two in style approaches for non-parametric density estimation. Histograms produce density estimates by computing the normalized frequency of factors inside every distinct bin of the information. KDEs are “smoothed” histograms that estimate the density at a given level by computing a weighted sum of its surrounding factors, the place neighbors are weighted in proportion to their distance.
- Non-parametric density estimation might be utilized to classification algorithms that require modeling the characteristic densities for every goal class (Bayesian classification). Classifiers constructed utilizing non-parametric density estimates might be able to outline extra versatile choice boundaries at the price of increased variance.
Take a look at the sources under in case you’re involved in studying extra!
The creator has created all photos on this article.
Sources
Studying Sources:
Datasets:
- Fisher, R. (1936). Iris [Dataset]. UCI Machine Studying Repository. https://doi.org/10.24432/C56C76. (CC BY 4.0)