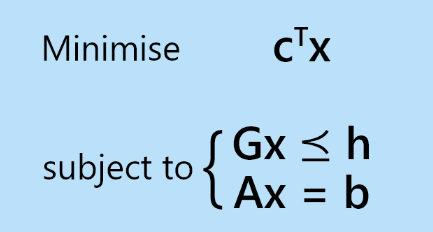Whereas CVXOPT offers a strong mathematical strategy to fixing Linear Programming (LP) issues, the graphical technique presents a visible illustration of the possible area and optimum resolution. This strategy is especially helpful for two-variable LP issues, permitting us to see how constraints work together and the place the optimum resolution lies.
The graphical technique solves an LP drawback by plotting its constraints and figuring out the possible area, which represents all doable options that fulfill the constraints. The optimum resolution is discovered at a vertex (nook level) of this possible area.
💡 When to Use the Graphical Methodology?
✅ Works finest for two-variable LP issues (straightforward to visualise in 2D).
✅ Helps perceive constraint interactions and feasibility.
✅ Helpful for educating and verifying options from algebraic solvers.
⚠️ Limitations:
❌ Not scalable past two variables (3D visualization is troublesome, and better dimensions can’t be plotted).
❌ Much less environment friendly for large-scale issues in comparison with mathematical solvers like CVXOPT.
- Importing Required Libraries
from sympy import symbols, Eq, remedy, N # For fixing linear equations
import numpy as np # For numerical operations
import matplotlib.pyplot as plt # For visualization
from scipy.optimize import linprog # To compute the optimum resolution
from scipy.spatial import ConvexHull # For locating the possible area
import warnings
warnings.filterwarnings("ignore") # Suppress warnings
2. Outline the Variables
x, y = symbols('x y')
- This defines x and y as the 2 determination variables.
3. Get Person Enter for the Goal Perform and Constraints
# Perform to get consumer enter for the target perform
def get_objective_function():
obj_x = float(enter("Enter the coefficient for x within the goal perform: "))
obj_y = float(enter("Enter the coefficient for y within the goal perform: "))
return obj_x, obj_y# Perform to get consumer enter for constraints
def get_constraints():
constraints = []
num_constraints = int(enter("Enter the variety of constraints: "))
for _ in vary(num_constraints):
coeff_x = float(enter("Enter the coefficient for x within the constraint: "))
coeff_y = float(enter("Enter the coefficient for y within the constraint: "))
signal = enter("Enter the inequality signal (=): ")
rhs = float(enter("Enter the right-hand aspect worth: "))
if signal == " constraints.append((coeff_x, coeff_y, rhs, " elif signal == ">=":
constraints.append((coeff_x, coeff_y, rhs, ">="))
return constraints
# Get consumer enter for the target perform and constraints
obj_x, obj_y = get_objective_function()
constraints = get_constraints()
4. Clear up for Intersection Factors
corner_points = []
for i in vary(len(constraints)):
for j in vary(i + 1, len(constraints)):
coeffs1 = constraints[i]
coeffs2 = constraints[j]
expr1 = Eq(coeffs1[0] * x + coeffs1[1] * y, coeffs1[2])
expr2 = Eq(coeffs2[0] * x + coeffs2[1] * y, coeffs2[2])
resolution = remedy((expr1, expr2), (x, y))
if resolution:
corner_points.append((N(resolution[x]), N(resolution[y])))
- This solves the system of equations for every pair of constraints to search out intersection factors.
- (x, y) values at these intersections are potential nook factors of the possible area.
5. Filter Out Infeasible Factors
# Filter out factors that do not fulfill all constraints
feasible_points = []
for level in corner_points:
if all(
(coeffs[0] * level[0] + coeffs[1] * level[1] = coeffs[2])
for coeffs in constraints
):
feasible_points.append(level)
- This filters out factors that don’t fulfill all constraints.
6. Plot the Constraint Strains
# Outline the target perform
def objective_function(x_val, y_val):
return obj_x * x_val + obj_y * y_val# Generate x and y values for plotting
x_vals = np.linspace(-20, 20, 1000)
y_vals = np.linspace(-20, 20, 1000)
X, Y = np.meshgrid(x_vals, y_vals)
# Plot the possible area and constraints
plt.determine()
colours = ['b', 'g', 'r', 'c', 'm', 'y', 'cyan', 'pink', 'darkviolet', 'lime', 'peru']
for idx, coeffs in enumerate(constraints):
coeff_x, coeff_y, rhs, signal = coeffs
if coeff_y != 0:
y_line = (rhs - coeff_x * x_vals) / coeff_y
else:
y_line = np.full_like(x_vals, rhs / coeff_x)
plt.plot(x_vals, y_line, label=f'Constraint {idx + 1}', colour=colours[idx % len(colors)])
# Plot x = 0 and y = 0 traces
plt.axvline(x=0, colour='black', label='x = 0')
plt.axhline(y=0, colour='black', label='y = 0')
- Every constraint is plotted as a straight line.
- Completely different colours assist differentiate constraints.
7. Fill the Possible Area
# Fill the possible area
if feasible_points:
feasible_points = np.array(feasible_points, dtype=float)
if len(feasible_points) >= 3:
hull = feasible_points[ConvexHull(feasible_points).vertices]
plt.fill(hull[:, 0], hull[:, 1], 'gray', alpha=0.5)
else:
print('Not sufficient possible factors to assemble the convex hull')
8. Compute the Optimum Answer Utilizing SciPy
# Use linprog to search out the optimum resolution
c = [obj_x, obj_y]
A = []
b = []
for coeff_x, coeff_y, rhs, register constraints:
if signal == " A.append([coeff_x, coeff_y])
b.append(rhs)
elif signal == ">=":
A.append([-coeff_x, -coeff_y])
b.append(-rhs)consequence = linprog(c, A_ub=A, b_ub=b, technique='simplex') #technique = 'simplex': Use the simplex technique to unravel linear programming issues
- SciPy’s
linprogperform computes the optimum resolution utilizing the Simplex technique.
9. Show the Optimum Answer and the Ultimate Plot
if consequence.success:
optimal_point = consequence.x
optimal_value = consequence.enjoyable
ask = enter('Do you need to print variety of iterations, optimum level and optimum worth? (sure/no): ')
if ask == 'sure':
optimization_type = enter("What kind of the target perform? (max/min): ")
if optimization_type == 'max':
optimal_value = -optimal_value
else:
optimal_value = optimal_value
print('optimal_point:', optimal_point)
print('optimal_value:', optimal_value)
print('Complete variety of iterations:', consequence.nit)# Plot the optimum resolution
plt.plot(optimal_point[0], optimal_point[1], 'ro', label='Optimum Answer')
plt.annotate(f'({optimal_point[0]}, {optimal_point[1]})', (optimal_point[0], optimal_point[1]), textcoords="offset factors", xytext=(-10,-10), ha='middle')
plt.legend(loc="decrease proper")
else:
print('No possible resolution')
plt.legend(loc="decrease proper")
# Set plot limits and labels
plt.xlim((-20, 20))
plt.ylim((-20, 20))
plt.xlabel('x')
plt.ylabel('y')
plt.title('Possible Area and Optimum Answer')
plt.present()
10. Instance Enter & Output:
We think about the identical LP drawback as earlier than:
📌 Instance Downside
Enter for the Goal Perform:
Be aware: rework the issue by changing maximization into minimization: max f(x)= -min -f(x)
Enter for Constraints:
Ask for print variety of iterations, optimum level and optimum worth:
Ultimate plot:
Ultimate output exhibits:
✅ Possible Area
✅ Constraint Strains
✅ Optimum Answer