are elementary objects in varied fields of recent pc science and arithmetic, together with however not restricted to linear Algebra, machine studying, and pc graphics.
Within the present collection of 4 tales, I’ll current a manner of decoding algebraic matrices in order that the bodily which means of assorted Matrix evaluation formulation will turn into clearer. For instance, the components for multiplying 2 matrices:
[begin{equation}
c_{i,j} = sum_{k=1}^{p} a_{i,k}*b_{k,j}
end{equation}]
or the components for inverting a series of matrices:
[begin{equation}
(ABC)^{-1} = C^{-1}B^{-1}A^{-1}
end{equation}]
Most likely for many of us, once we have been studying matrix-related definitions and formulation for the primary time, questions like the next ones arose:
- what does a matrix truly symbolize,
- what’s the bodily which means of multiplying a matrix by a vector,
- why multiplication of two matrices is carried out by such a non-standard components,
- why for multiplication the variety of columns of the primary matrix should be equal to the variety of rows of the second,
- what’s the which means of transposing a matrix,
- why for sure kinds of matrices, inversion equals to transposition,
- … and so forth.
On this collection, I plan to current a method of answering a lot of the listed questions. So let’s dive in!
However earlier than beginning, listed here are a few notation guidelines that I exploit all through this collection:
- Matrices are denoted by uppercase (like A, B), whereas vectors and scalars are denoted by lowercase (like x, y or m, n),
- ai,j – The worth of i-th row and j-th column of matrix ‘A‘,
- xi – the i-th worth of vector ‘x‘.
Multiplication of a matrix by a vector
Let’s put apart for now the best operations on matrices, that are addition and subtraction. The following easiest manipulation might be the multiplication of a matrix by a vector:
[begin{equation}
y = Ax
end{equation}]
We all know that the results of such an operation is one other vector ‘y‘, which has a size equal to the variety of rows of ‘A‘, whereas the size of ‘x‘ needs to be equal to the variety of columns of ‘A‘.
Let’s consider “n*n” sq. matrices for now (these with equal numbers of rows and columns). We are going to observe the conduct of rectangular matrices a bit later.
The components for calculating yi is:
[begin{equation}
y_i = sum_{j=1}^{n} a_{i,j}*x_j
end{equation}]
… which, if written within the expanded manner, is:
[begin{equation}
begin{cases}
y_1 = a_{1,1}x_1 + a_{1,2}x_2 + dots + a_{1,n}x_n
y_2 = a_{2,1}x_1 + a_{2,2}x_2 + dots + a_{2,n}x_n
;;;;; vdots
y_n = a_{n,1}x_1 + a_{n,2}x_2 + dots + a_{n,n}x_n
end{cases}
end{equation}]
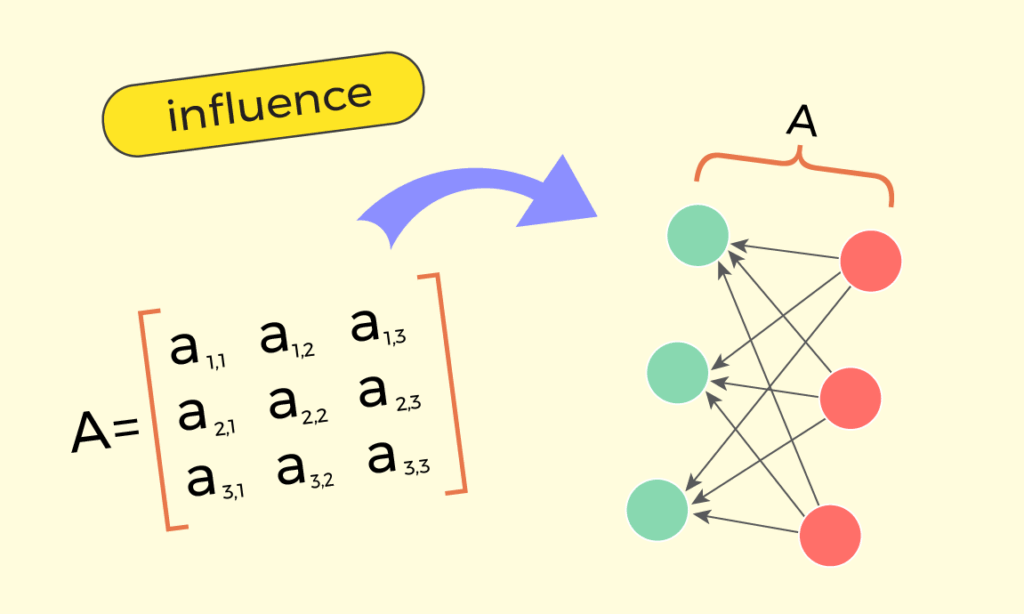
Such expanded notation clearly reveals that each cell ai,j is current within the system of equations solely as soon as. Extra exactly, ai,j is current because the issue of xj, and participates solely within the sum of yi. This leads us to the next interpretation:
Within the product of a matrix by a vector “y = Ax”, a sure cell ai,j describes how a lot the output worth yi is affected by the enter worth xj.
Having that mentioned, we are able to draw the matrix geometrically, within the following manner:
And as we’re going to interpret matrix ‘A‘ as influences of values xj on values yi, it’s cheap to connect values of ‘x‘ to the suitable stack, which is able to end in values of ‘y‘ being current on the left stack.

I choose to name this interpretation of matrices as “X-way interpretation”, as the position of introduced arrows seems to be just like the English letter “X”. And for a sure matrix ‘A‘, I choose to name such a drawing as “X-diagram” of ‘A‘.
Such interpretation clearly reveals that the enter vector ‘x‘ goes by means of some type of transformation, from proper to left, and turns into vector ‘y‘. That is the explanation why in Linear Algebra, matrices are additionally referred to as “transformation matrices”.
If taking a look at any ok-th merchandise of the left stack, we are able to see how all of the values of ‘x‘ are being accrued in the direction of it, whereas being multiplied by coefficients aok,j (that are the ok-th row of the matrix).


On the identical time, if taking a look at any ok-th merchandise of the suitable stack, we are able to see how the worth xok is being distributed over all values of ‘y’, whereas being multiplied by coefficients ai,ok (which at the moment are the ok-th column of the matrix).


This already provides us one other perception, that when decoding a matrix within the X-way, the left stack may be related to rows of the matrix, whereas the suitable stack may be related to its columns.
Absolutely, if we’re concerned about finding some worth ai,j, taking a look at its X-diagram just isn’t as handy as trying on the matrix in its odd manner – as an oblong desk of numbers. However, as we’ll see later and within the subsequent tales of this collection, X-way interpretation explicitly presents the which means of assorted algebraic operations over matrices.
Rectangular matrices
Multiplication of the shape “y = Ax” is allowed provided that the size of vector ‘x‘ is the same as the variety of columns of matrix ‘A‘. On the identical time, the consequence vector ‘y‘ can have a size equal to the variety of rows of ‘A‘. So, if ‘A‘ is an oblong matrix, vector ‘x‘ will change its size whereas passing by means of its transformation. We will observe it by taking a look at X-way interpretation:


Now it’s clear why we are able to multiply ‘A‘ solely on such a vector ‘x‘, the size of which is the same as the variety of columns of ‘A‘: as a result of in any other case the vector ‘x‘ will merely not match on the suitable facet of the X-diagram.
Equally, it’s clear why the size of the consequence vector “y = Ax” is the same as the variety of rows of ‘A‘.
Viewing rectangular matrices within the X-way strokes, we’ve beforehand made an perception, which is that gadgets of the left stack of the X-diagram correspond to rows of the illustrated matrix, whereas gadgets of its proper stack correspond to columns.
Observing a number of particular matrices in X-way interpretation
Let’s see how X-way interpretation will assist us to grasp the conduct of sure particular matrices:
Scale / diagonal matrix
A scale matrix is such a sq. matrix that has all cells of its important diagonal equal to some worth ‘s‘, whereas having all different cells equal to 0. Multiplying a vector “x” by such a matrix leads to each worth of “x” being multiplied by ‘s‘:
[begin{equation*}
begin{pmatrix}
y_1 y_2 vdots y_{n-1} y_n
end{pmatrix}
=
begin{bmatrix}
s & 0 & dots & 0 & 0
0 & s & dots & 0 & 0
& & vdots
0 & 0 & dots & s & 0
0 & 0 & dots & 0 & s
end{bmatrix}
*
begin{pmatrix}
x_1 x_2 vdots x_{n-1} x_n
end{pmatrix}
=
begin{pmatrix}
s x_1 s x_2 vdots s x_{n-1} s x_n
end{pmatrix}
end{equation*}]
The X-way interpretation of a scale matrix reveals its bodily which means. As the one non-zero cells listed here are those on the diagonal – ai,i, the X-diagram can have arrows solely between corresponding pairs of enter and output values, that are xi and yi.

A particular case of a scale matrix is the diagonal matrix (additionally referred to as an “identification matrix”), usually denoted with the letters “E” or “I” (we’ll use “E” within the present writing). It’s a scale matrix with the parameter “s=1″.
[begin{equation*}
begin{pmatrix}
y_1 y_2 vdots y_{n-1} y_n
end{pmatrix}
=
begin{bmatrix}
1 & 0 & dots & 0 & 0
0 & 1 & dots & 0 & 0
& & vdots
0 & 0 & dots & 1 & 0
0 & 0 & dots & 0 & 1
end{bmatrix}
*
begin{pmatrix}
x_1 x_2 vdots x_{n-1} x_n
end{pmatrix}
=
begin{pmatrix}
x_1 x_2 vdots x_{n-1} x_n
end{pmatrix}
end{equation*}]

We see that doing the multiplication “y = Ex” will simply go away the vector ‘x‘ unchanged, as each worth xi is simply multiplied by 1.
90° rotation matrix
A matrix, which rotates a given level (x1, x2) across the zero-point (0,0) by 90 levels counter-clockwise, has a easy kind:
[begin{equation*}
begin{pmatrix}
y_1 y_2
end{pmatrix}
=
begin{bmatrix}
0 & -1
1 & phantom{-}0
end{bmatrix}
*
begin{pmatrix}
x_1 x_2
end{pmatrix}
=
begin{pmatrix}
-x_2 phantom{-}x_1
end{pmatrix}
end{equation*}]

X-way interpretation of the 90° rotation matrix reveals that conduct:

Trade matrix
An alternate matrix ‘J‘ is such a matrix that has 1s on its anti-diagonal, and has 0s in any respect different cells. Multiplying it by a vector ‘x‘ leads to reversing the order of values of ‘x‘:
[begin{equation*}
begin{pmatrix}
y_1 y_2 vdots y_{n-1} y_n
end{pmatrix}
=
begin{bmatrix}
0 & 0 & dots & 0 & 1
0 & 0 & dots & 1 & 0
& & vdots
0 & 1 & dots & 0 & 0
1 & 0 & dots & 0 & 0
end{bmatrix}
*
begin{pmatrix}
x_1 x_2 vdots x_{n-1} x_n
end{pmatrix}
=
begin{pmatrix}
x_n x_{n-1} vdots x_2 x_1
end{pmatrix}
end{equation*}]
This truth is explicitly proven within the X-way interpretation of the alternate matrix ‘J‘:

The 1s reside solely on the anti-diagonal right here, which implies that output worth y1 is affected solely by enter worth xn, then y2 is affected solely by xn-1, and so forth, having yn affected solely by x1. That is seen on the X-diagram of the alternate matrix ‘J‘.
Shift matrix
A shift matrix is such a matrix that has 1s on some diagonal, parallel to the primary diagonal, and has 0s in any respect remaining cells:
[begin{equation*}
begin{pmatrix}
y_1 y_2 y_3 y_4 y_5
end{pmatrix}
=
begin{bmatrix}
0 & 1 & 0 & 0 & 0
0 & 0 & 1 & 0 & 0
0 & 0 & 0 & 1 & 0
0 & 0 & 0 & 0 & 1
0 & 0 & 0 & 0 & 0
end{bmatrix}
*
begin{pmatrix}
x_1 x_2 x_3 x_4 x_5
end{pmatrix}
=
begin{pmatrix}
x_2 x_3 x_4 x_5 0
end{pmatrix}
end{equation*}]
Multiplying such a matrix by a vector “x” leads to the identical vector however all values shifted by ‘ok‘ positions up or down. ‘ok‘ is the same as the space between the diagonal with 1s and the primary diagonal. Within the introduced instance, we’ve “ok=1″ (diagonal with 1s is just one place above the primary diagonal). If the diagonal with 1s is within the upper-right triangle, as it’s within the introduced instance, then the shift of values of “x” is carried out upwards. In any other case, the shift of values is carried out downwards.
Shift matrix will also be illustrated explicitly within the X-way:

Permutation matrix
A permutation matrix is a matrix composed of 0s and 1s, which rearranges all values of the enter vector “x” in a sure manner. The impression is that when multiplied by such a matrix, the values of “x” are being permuted.
To attain that, the n*n-sized permutation matrix ‘P‘ should have ‘n‘ 1s, whereas all different cells should be 0. Additionally, no two 1s should seem in the identical row or the identical column. An instance of a permutation matrix is:
[begin{equation*}
begin{pmatrix}
y_1 y_2 y_3 y_4 y_5
end{pmatrix}
=
begin{bmatrix}
0 & 0 & 0 & 1 & 0
1 & 0 & 0 & 0 & 0
0 & 0 & 0 & 0 & 1
0 & 0 & 1 & 0 & 0
0 & 1 & 0 & 0 & 0
end{bmatrix}
*
begin{pmatrix}
x_1 x_2 x_3 x_4 x_5
end{pmatrix}
=
begin{pmatrix}
x_4 x_1 x_5 x_3 x_2
end{pmatrix}
end{equation*}]
If drawing the X-diagram of the talked about permutation matrix ‘P‘, we’ll see the reason of such conduct:

The constraint that no two 1s should seem in the identical column implies that just one arrow ought to depart from any merchandise of the suitable stack. The constraint that no two 1s should seem on the identical row implies that just one arrow should arrive at each merchandise of the left stack. Lastly, the constraint that each one the non-zero cells of a permutation matrix should be 1 implies that a sure enter worth xj, whereas arriving at output worth yi, won’t be multiplied by any coefficient. All this leads to the values of vector “x” being rearranged in a sure method.
Triangular matrix
A triangular matrix is a matrix that has 0s in any respect cells both beneath or above its important diagonal. Let’s observe upper-triangular matrices (the place 0s are beneath the primary diagonal), because the lower-triangular ones have related properties.
[
begin{equation*}
begin{pmatrix}
y_1 y_2 y_3 y_4
end{pmatrix}
=
begin{bmatrix}
a_{1,1} & a_{1,2} & a_{1,3} & a_{1,4}
0 & a_{2,2} & a_{2,3} & a_{2,4}
0 & 0 & a_{3,3} & a_{3,4}
0 & 0 & 0 & a_{4,4}
end{bmatrix}
*
begin{pmatrix}
x_1 x_2 x_3 x_4
end{pmatrix}
=
begin{pmatrix}
begin{aligned}
a_{1,1}x_1 + a_{1,2}x_2 + a_{1,3}x_3 + a_{1,4}x_4
a_{2,2}x_2 + a_{2,3}x_3 + a_{2,4}x_4
a_{3,3}x_3 + a_{3,4}x_4
a_{4,4}x_4
end{aligned}
end{pmatrix}
end{equation*}
]
Such an expanded notation illustrates that any output worth yi is affected solely by enter values with larger or equal indexes, that are xi, xi+1, xi+2, …, xN. If drawing the X-diagram of the talked about upper-triangular matrix, that truth turns into apparent:

Conclusion
Within the first story of the collection, which is dedicated to the interpretation of algebraic matrices, we checked out how matrices may be introduced geometrically, and referred to as it “X-way interpretation”. Such interpretation explicitly highlights varied properties of matrix-vector multiplication, in addition to the conduct of matrices of a number of particular varieties.
Within the subsequent story of this collection, we’ll discover an interpretation of the multiplication of two matrices by working on their X-diagrams, so keep tuned for the second arrival!
My gratitude to:
– Roza Galstyan, for cautious evaluate of the draft,
– Asya Papyan, for the exact design of all of the used illustrations ( https://www.behance.net/asyapapyan ).In case you loved studying this story, be at liberty to attach with me on LinkedIn, the place, amongst different issues, I may also submit updates ( https://www.linkedin.com/in/tigran-hayrapetyan-cs/ ).
All used photographs, except in any other case famous, are designed by request of the creator.