is a cornerstone method for modeling tabular knowledge attributable to its pace and ease. It delivers nice outcomes with none fuss. If you go searching you’ll see a number of choices like LightGBM, XGBoost, and so forth. Catboost is one such variant. On this publish, we’ll take an in depth have a look at this mannequin, discover its interior workings, and perceive what makes it an incredible alternative for real-world duties.
Goal Statistic
Goal Encoding Instance: the typical worth of the goal variable for a class is used to switch every class
One of many vital contributions of the CatBoost paper is a brand new technique of calculating the Goal Statistic. What’s a Goal Statistic? If in case you have labored with categorical variables earlier than, you’d know that essentially the most rudimentary technique to take care of categorical variables is to make use of one-hot encoding. From expertise, you’d additionally know that this introduces a can of issues like sparsity, curse of dimensionality, reminiscence points, and so forth. Particularly for categorical variables with excessive cardinality.
Grasping Goal Statistic
To keep away from one-hot encoding, we calculate the Goal Statistic as a substitute for the explicit variables. This implies we calculate the imply of the goal variable at every distinctive worth of the explicit variable. So if a categorical variable takes the values — A, B, C then we’ll calculate the typical worth of (textual content{y}) over all these values and substitute these values with the typical of (textual content{y}) at every distinctive worth.
That sounds good, proper? It does however this strategy comes with its issues — specifically Goal Leakage. To grasp this, let’s take an excessive instance. Excessive examples are sometimes the simplest technique to eke out points within the strategy. Contemplate the beneath dataset:
| Categorical Column | Goal Column |
|---|---|
| A | 0 |
| B | 1 |
| C | 0 |
| D | 1 |
| E | 0 |
Now let’s write the equation for calculating the Goal Statistic:
[hat{x}^i_k = frac{
sum_{j=1}^{n} 1_{{x^i_j = x^i_k}} cdot y_j + a p
}{
sum_{j=1}^{n} 1_{{x^i_j = x^i_k}} + a
}]
Right here (x^i_j) is the worth of the i-th categorical function for the j-th pattern. So for the k-th pattern, we iterate over all samples of (x^i), choose those having the worth (x^i_k), and take the typical worth of (y) over these samples. As a substitute of taking a direct common, we take a smoothened common which is what the (a) and (p) phrases are for. The (a) parameter is the smoothening parameter and (p) is the worldwide imply of (y).
If we calculate the Goal Statistic utilizing the formulation above, we get:
| Categorical Column | Goal Column | Goal Statistic |
|---|---|---|
| A | 0 | (frac{ap}{1+a}) |
| B | 1 | (frac{1+ap}{1+a}) |
| C | 0 | (frac{ap}{1+a}) |
| D | 1 | (frac{1+ap}{1+a}) |
| E | 0 | (frac{ap}{1+a}) |
Now if I exploit this Goal Statistic column as my coaching knowledge, I’ll get an ideal break up at ( threshold = frac{0.5+ap}{1+a}). Something above this worth will probably be labeled as 1 and something beneath will probably be labeled as 0. I’ve an ideal classification at this level, so I get 100% accuracy on my coaching knowledge.
Let’s check out the take a look at knowledge. Right here, since we’re assuming that the function has all distinctive values, the Goal Statistic turns into—
[TS = frac{0+ap}{0+a} = p]
If (threshold) is bigger than (p), all take a look at knowledge predictions will probably be (0). Conversely, if (threshold) is lower than (p), all take a look at knowledge predictions will probably be (1) resulting in poor efficiency on the take a look at set.
Though we hardly ever see datasets the place values of a categorical variable are all distinctive, we do see instances of excessive cardinality. This excessive instance exhibits the pitfalls of utilizing Grasping Goal Statistic as an encoding strategy.
Depart One Out Goal Statistic
So the Grasping TS didn’t work out fairly properly for us. Let’s strive one other technique— the Depart One Out Goal Statistic technique. At first look, this appears promising. However, because it seems, this too has its issues. Let’s see how with one other excessive instance. This time let’s assume that our categorical variable (x^i) has just one distinctive worth, i.e., all values are the identical. Contemplate the beneath knowledge:
| Categorical Column | Goal Column |
|---|---|
| A | 0 |
| A | 1 |
| A | 0 |
| A | 1 |
If calculate the depart one out goal statistic, we get:
| Categorical Column | Goal Column | Goal Statistic |
|---|---|---|
| A | 0 | (frac{n^+ -y_k + ap}{n+a}) |
| A | 1 | (frac{n^+ -y_k + ap}{n+a}) |
| A | 0 | (frac{n^+ -y_k + ap}{n+a}) |
| A | 1 | (frac{n^+ -y_k + ap}{n+a}) |
Right here:
(n) is the entire samples within the knowledge (in our case this 4)
(n^+) is the variety of optimistic samples within the knowledge (in our case this 2)
(y_k) is the worth of the goal column in that row
Substituting the above, we get:
| Categorical Column | Goal Column | Goal Statistic |
|---|---|---|
| A | 0 | (frac{2 + ap}{4+a}) |
| A | 1 | (frac{1 + ap}{4+a}) |
| A | 0 | (frac{2 + ap}{4+a}) |
| A | 1 | (frac{1 + ap}{4+a}) |
n and n+Now, if I exploit this Goal Statistic column as my coaching knowledge, I’ll get an ideal break up at ( threshold = frac{1.5+ap}{4+a}). Something above this worth will probably be labeled as 0 and something beneath will probably be labeled as 1. I’ve an ideal classification at this level, so I once more get 100% accuracy on my coaching knowledge.
You see the issue, proper? My categorical variable which doesn’t have greater than a novel worth is producing completely different values for Goal Statistic which can carry out nice on the coaching knowledge however will fail miserably on the take a look at knowledge.
Ordered Goal Statistic

CatBoost introduces a method referred to as Ordered Goal Statistic to deal with the problems mentioned above. That is the core precept of CatBoost’s dealing with of categorical variables.
This technique, impressed by on-line studying, makes use of solely previous knowledge to make predictions. CatBoost generates a random permutation (random ordering) of the coaching knowledge((sigma)). To compute the Goal Statistic for a pattern at row (okay), CatBoost makes use of samples from row (1) to (k-1). For the take a look at knowledge, it makes use of your complete prepare knowledge to compute the statistic.
Moreover, CatBoost generates a brand new permutation for every tree, quite than reusing the identical permutation every time. This reduces the variance that may come up within the early samples.
Ordered Boosting

One other vital innovation launched by the CatBoost paper is its use of Ordered Boosting. It builds on related ideas as ordered goal statistics, the place CatBoost randomly permutes the coaching knowledge initially of every tree and makes predictions sequentially.
In conventional boosting strategies, when coaching tree (t), the mannequin makes use of predictions from the earlier tree (t−1) for all coaching samples, together with the one it’s at present predicting. This will result in goal leakage, because the mannequin could not directly use the label of the present pattern throughout coaching.
To handle this subject, CatBoost makes use of Ordered Boosting the place, for a given pattern, it solely makes use of predictions from earlier rows within the coaching knowledge to calculate gradients and construct timber. For every row (i) within the permutation, CatBoost calculates the output worth of a leaf utilizing solely the samples earlier than (i). The mannequin makes use of this worth to get the prediction for row (i). Thus, the mannequin predicts every row with out taking a look at its label.
CatBoost trains every tree utilizing a brand new random permutation to common the variance in early samples in a single permutation.
Let’s say we’ve 5 knowledge factors: A, B, C, D, E. CatBoost creates a random permutation of those factors. Suppose the permutation is: σ = [C, A, E, B, D]
| Step | Information Used to Prepare | Information Level Being Predicted | Notes |
|---|---|---|---|
| 1 | — | C | No earlier knowledge → use prior |
| 2 | C | A | Mannequin skilled on C solely |
| 3 | C, A | E | Mannequin skilled on C, A |
| 4 | C, A, E | B | Mannequin skilled on C, A, E |
| 5 | C, A, E, B | D | Mannequin skilled on C, A, E, B |
This avoids utilizing the precise label of the present row to get the prediction thus stopping leakage.
Constructing a Tree
Every time CatBoost builds a tree, it creates a random permutation of the coaching knowledge. It calculates the ordered goal statistic for all the explicit variables with greater than two distinctive values. For a binary categorical variable, it maps the values to zeros and ones.
CatBoost processes knowledge as if the information is arriving sequentially. It begins with an preliminary prediction of zero for all situations, that means the residuals are initially equal to the goal values.
As coaching proceeds, CatBoost updates the leaf output for every pattern utilizing the residuals of the earlier samples that fall into the identical leaf. By not utilizing the present pattern’s label for prediction, CatBoost successfully prevents knowledge leakage.
Cut up Candidates

On the core of a choice tree lies the duty of choosing the optimum function and threshold for splitting a node. This includes evaluating a number of feature-threshold combos and deciding on the one that provides one of the best discount in loss. CatBoost does one thing related. It discretizes the continual variable into bins to simplify the seek for the optimum mixture. It evaluates every of those feature-bin combos to find out one of the best break up
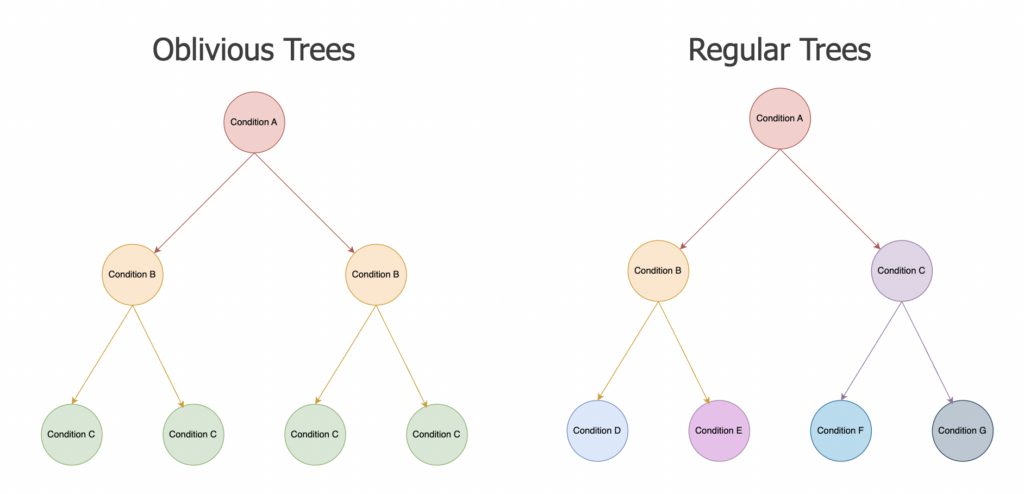
CatBoost makes use of Oblivious Bushes, a key distinction in comparison with different timber, the place it makes use of the identical break up throughout all nodes on the similar depth.
Oblivious Bushes

In contrast to commonplace resolution timber, the place completely different nodes can break up on completely different circumstances (feature-threshold), Oblivious Bushes break up throughout the identical circumstances throughout all nodes on the similar depth of a tree. At a given depth, all samples are evaluated on the similar feature-threshold mixture. This symmetry has a number of implications:
- Pace and ease: for the reason that similar situation is utilized throughout all nodes on the similar depth, the timber produced are easier and sooner to coach
- Regularization: Since all timber are pressured to use the identical situation throughout the tree on the similar depth, there’s a regularization impact on the predictions
- Parallelization: the uniformity of the break up situation, makes it simpler to parallelize the tree creation and utilization of GPU to speed up coaching
Conclusion
CatBoost stands out by immediately tackling a long-standing problem: how you can deal with categorical variables successfully with out inflicting goal leakage. By improvements like Ordered Goal Statistics, Ordered Boosting, and the usage of Oblivious Bushes, it effectively balances robustness and accuracy.
For those who discovered this deep dive useful, you would possibly get pleasure from one other deep dive on the variations between Stochastic Gradient Classifer and Logistic Regression